次世代信号情報処理シリーズ 7 テンソルデータ解析の基礎と応用 - テンソル表現，縮約計算，テンソル分解と低ランク近似 -

次世代信号情報処理シリーズ 7

テンソルデータ解析の基礎と応用 - テンソル表現，縮約計算，テンソル分解と低ランク近似 -

田中聡久東京農工大教授博士（工学）監修
横田達也名工大准教授博士（工学）著

線形代数の復習をしながら，テンソル分解の基礎から応用を学べる。

ジャンル

発行年月日: 2024/06/28

判型: A5

ページ数: 264ページ

ISBN: 978-4-339-01407-5

在庫あり

2営業日以内に出荷致します。

定価

4,400円(本体4,000円+税)

カートに入れる

購入案内

内容紹介
まえがき
目次
レビュー
著者紹介
書籍紹介・書評掲載情報
広告掲載情報

【書籍の特徴】
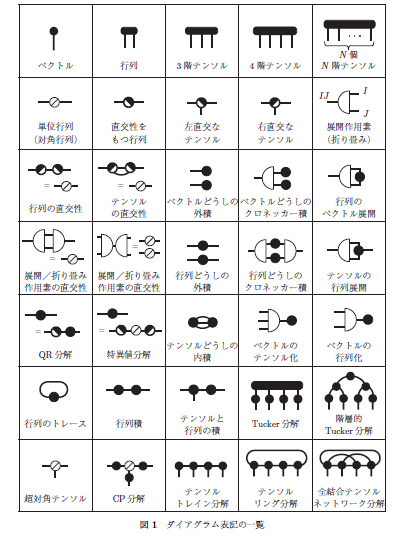
本書はテンソル分解の入門書として書きました。テンソルの基礎，線形代数の基礎，主成分分析，テンソル分解の基礎，テンソル分解の応用までを滑らかにつなぐことを心がけました。テンソルネットワークでよく用いられるダイアグラム表記も積極的に取り入れて解説しています。

【本書の構成】
1章：「情報のテンソル表現」では，ベクトル，行列，テンソルの簡単な導入と応用事例について広く浅くまとめました。情報が意味するものは，音声，脳波，画像，自然言語など多種多様です。これらのデータはさまざまな形式で保存されていますが，テンソルを使って表現すると，それに対してさまざまなテンソルデータ解析の手法を適用できるようになります。
2章：「テンソルの変形と計算」では，テンソルどうしの積（縮約）を理解することを最終目標に，テンソルの基本的な操作（ベクトル展開，行列展開，折り畳み，アダマール積，クロネッカー積など）を丁寧に紹介していきます。
3章：「線形代数と主成分分析」では，前半は線形代数の簡潔なハイライトになっています。内積，外積，ノルム，列空間，直交化，射影，固有値分解，特異値分解，行列ランクなどの内容を一通り学び直すことができます。エッカート・ヤングの定理の証明，べき乗法や縮退処理を用いた特異値分解のアルゴリズムについて紹介している点が特色です。後半ではこれらの応用として主成分分析の紹介と，それをコンピュータを用いてどのように行うのか（アルゴリズム）について説明していきます。
4章：「テンソル分解」では，CP分解，Tucker分解，TT分解を紹介し，それに基づいてテンソルのCPランク，Tuckerランク，TTランクについて説明します。また，各テンソル分解によってテンソルの低ランク近似を得るための基本アルゴリズムについて解説します。他のテンソル分解モデルについては代表的なものを紹介する程度にしています。
5章：「テンソルデータ解析」では，テンソル分解を実際のデータ分析課題へ適用するための方法論について紹介しました。観測モデル，誤差関数，制約付きテンソル分解などの組合せで多様な問題設定が考えられることがおわかりいただけると思います。

【著者からのメッセージ】
本書を理解するうえで必要な数学的知識は線形代数+αのみです。線形代数への愛着と理解が深まるほど，テンソル分解への理解も深まるといえます。また，本書ではMATLABプログラムの例をたくさん載せています。自分でプログラムが書ける，そしてきちんと動く，というのは少なくとも処理の流れは具体的に，かつ正確に理解できていることの証だと思います。手を動かしながら読んでいただき，具体的な理解につなげていだだければと思います。

本書はテンソル分解の入門書として書きました。テンソルの基礎，線形代数の基礎，主成分分析，テンソル分解の基礎，テンソル分解の応用までを滑らかにつなぐことを心がけました。テンソルネットワークでよく用いられるダイアグラム表記（図1）も積極的に取り入れて解説しています。本書を理解するうえで必要な数学的知識は線形代数+αのみです。線形代数への愛着と理解が深まるほど，テンソル分解への理解も深まるといえます。

第1章ではベクトル，行列，テンソルの簡単な導入と応用事例について広く浅くまとめました。

第2章ではテンソルの変形と計算について解説しました。テンソルのベクトル化，行列展開，折り畳みなどは通常（特に論文上では）簡単な紹介だけにして細かい定義をうやむやにしてしまう操作ですが，本書ではこれらを不足なく定義することを試みています（そのため説明がくどいと感じるかもしれません）。テンソルの計算に関しては，基本的な四則演算，特殊な行列積，テンソル積，テンソルネットワークなどについて解説しています。

第3章前半は線形代数の簡潔なハイライトになっています。内積，外積，ノルム，列空間，直交化，射影，固有値分解，特異値分解，行列ランクなどの内容を一通り学び直すことができます。エッカート・ヤングの定理の証明，べき乗法や縮退処理を用いた特異値分解のアルゴリズムについて紹介している点が特色です。第3章後半ではこれらの応用として主成分分析を解説します。

第4章ではテンソルのランク1分解，CP分解，Tucker分解，テンソルトレイン分解に絞って解説をしました。他のテンソル分解モデルについては代表的なものを紹介する程度にしています。理論が追えたとしても実際にプログラムを作ろうとすると手が止まってしまう（または思ったとおりに動かない），ということはよくあると思います。これは抽象的には理解していても，細かい部分の具体的な理解が足りていないことの表れです。自分でプログラムが書ける（そしてきちんと動く），というのは少なくとも処理の流れは具体的に，かつ正確に理解できていることの証だと思います。本書ではMATLABプログラムの例をたくさん載せています。手を動かしながら読んでいただき，具体的な理解につなげていだだければと思います。

第5章ではテンソル分解を実際のデータ分析課題へ適用するための方法論について大風呂敷を広げて紹介しました。観測モデル，誤差関数，制約付きテンソル分解などの組合せで多様な問題設定が考えられることがおわかりいただけると思います。任意の組合せに対応できるような万能なアルゴリズムは現状存在しませんが，テンソル分解の研究が進むに従ってデータ分析の道具としての使いやすさも年々よくなっていくと信じます。

数年前から筆者が研究室を主宰するようになったこともあり，学生が線形代数の復習をしつつテンソル分解の基礎を学べるような丁度よい本があると嬉しい（しかしなかなかよい本が見つからない）と思っていました。それならば自分で書くしかない，と思い始めていたところタイミングよく東京農工大学の田中聡久先生から本書執筆の話をいただけたのはきわめて幸運なことでした。また，執筆にあたり田中先生からは本書の魅力が増すような多くのアドバイスをいただきました。心より御礼申し上げます。

山岸昌夫先生（法政大学）からは原稿に対して理論や数式の厳密性，説明不足な点の指摘など有益なコメントをたくさんいただきました。ありがとうございます。また，丁寧に編集してくださったコロナ社の皆様に感謝いたします。そして最後に，いつも筆者を支えてくれている家族のみんなに感謝の意を伝えたいと思います。

2024年4月
横田達也

1.　情報のテンソル表現
1.1　ベクトル，行列，テンソルの基礎
　1.1.1　ベクトル
　1.1.2　行列
　1.1.3　3階テンソル
　1.1.4　N階テンソル
　1.1.5　テンソルのイメージ
　1.1.6　テンソルのモード
　1.1.7　テンソルのダイアグラム表記
　1.1.8　プログラムの例
1.2　テンソル表現の事例紹介
　1.2.1　画像処理
　1.2.2　音響信号処理
　1.2.3　生体信号処理
　1.2.4　無線通信
　1.2.5　バイオインフォマティクス（生命情報処理）
　1.2.6　自然言語処理
　1.2.7　関係データ（グラフ）
　1.2.8　推薦システム
　1.2.9　交通データ
　1.2.10　確率質量関数
　1.2.11　回帰係数
　1.2.12　線形写像
章末問題

2.　テンソルの変形と計算
2.1　基礎知識
　2.1.1　数式の記法について
　2.1.2　テンソルの要素
　2.1.3　ファイバ
　2.1.4　スライス
　2.1.5　部分テンソル
　2.1.6　プログラムの例
2.2　テンソルの変形:
　2.2.1　転置（モード置換）
　2.2.2　ベクトル展開
　2.2.3　行列展開
　2.2.4　折り畳み（テンソル化）
　2.2.5　変形の線形性
　2.2.6　変形のダイアグラム表記
　2.2.7　プログラムの例
2.3　テンソルの計算
　2.3.1　和，差，スカラー倍
　2.3.2　要素ごとの積と商
　2.3.3　内積
　2.3.4　フロベニウスノルム
　2.3.5　外積
　2.3.6　行列積
　2.3.7　クロネッカー積
　2.3.8　カトリ・ラオ積
　2.3.9　テンソルと行列の積（モード積，縮約）
　2.3.10　テンソル積
　2.3.11　テンソルネットワークと計算量
　2.3.12　プログラムの例
章末問題

3.　線形代数と主成分分析
3.1　線形代数ハイライト
　3.1.1　列空間と左ゼロ空間
　3.1.2　直交行列と直交化
　3.1.3　列空間への射影
　3.1.4　固有値分解
　3.1.5　正定値行列
　3.1.6　逆行列
　3.1.7　特異値分解
　3.1.8　行列ノルム
　3.1.9　特異値分解と固有値分解の関係
　3.1.10　行列のランク
　3.1.11　行列の低ランク近似:
　3.1.12　エッカート・ヤングの定理の証明
　3.1.13　行列の最良ランク1近似と縮退処理
　3.1.14　べき乗法による最小ランク1近似
　3.1.15　特異値分解の原始的アルゴリズム
3.2　主成分分析
　3.2.1　次元削減としての主成分分析
　3.2.2　最適化問題の整理と分散最大化の特徴付け
　3.2.3　部分空間の最適化
　3.2.4　主成分分析の手順（まとめ）
　3.2.5　固有値，固有ベクトルの意味と寄与率
　3.2.6　主成分分析の適用例
章末問題

4.　テンソル分解
4.1　ランク1テンソル
　4.1.1　ランク1テンソルの定義と性質
　4.1.2　ランク1分解によるテンソルの表現
　4.1.3　ランク1分解の一意性
　4.1.4　テンソルのランク1近似
　4.1.5　べき乗法と交互最小二乗法
　4.1.6　プログラムの例
4.2　CP分解
　4.2.1　CP分解とCPランク
　4.2.2　CP分解の一意性
　4.2.3　CP分解に基づくテンソルの低ランク近似
　4.2.4　交互最小二乗アルゴリズムによるCP分解
　4.2.5　階層的交互最小二乗アルゴリズムによるCP分解
　4.2.6　プログラムの例
　4.2.7　CP分解の特徴
4.3　Tucker分解
　4.3.1　Tucker分解とTuckerランク
　4.3.2　Tucker分解の任意性
　4.3.3　高階特異値分解（HOSVD）
　4.3.4　交互最小二乗アルゴリズムによるTucker分解（直交制約なし）
　4.3.5　HOOIアルゴリズムによるTucker分解（直交制約あり）
　4.3.6　プログラムの例
　4.3.7　Tucker分解の特徴
4.4　テンソルトレイン分解
　4.4.1　テンソルトレイン（TT）分解
　4.4.2　k行列展開とTTランク
　4.4.3　特異値分解を用いたTT分解（TT-SVD）
　4.4.4　TT-SVDによる低ランク近似
　4.4.5　直交化されたTT分解
　4.4.6　TT分解のための交互最小二乗アルゴリズム
　4.4.7　プログラムの例
4.5　その他のテンソル分解モデル
　4.5.1　ブロックターム分解
　4.5.2　階層的Tucker分解
　4.5.3　テンソルリング分解
　4.5.4　全結合テンソルネットワーク分解
　4.5.5　同時テンソル分解
　4.5.6　対称テンソル分解
章末問題

5.　テンソルデータ解析
5.1　テンソルデータの線形観測モデルと逆問題
　5.1.1　線形観測モデル
　5.1.2　観測モデルに基づくデータ分析課題の分類
5.2　テンソルデータ解析の方法論
　5.2.1　観測モデルに基づく線形方程式の不良設定性
　5.2.2　ノルム最小化による再構成
　5.2.3　テンソルデータ解析問題の定式化
　5.2.4　誤差関数の種類
　5.2.5　ペナルティ関数の種類:
5.3　最適化の準備
　5.3.1　交互方向乗数法
　5.3.2　上界最小化（MM）アルゴリズム
　5.3.3　近接写像
5.4　欠損値を含むテンソルデータの分析
　5.4.1　核ノルムに基づく低ランク行列補完
　5.4.2　テンソル分解に基づく低ランクテンソル補完
　5.4.3　テンソル補完の応用事例
5.5　スパース成分を含むテンソルデータの分析
　5.5.1　ロバスト主成分分析
　5.5.2　ロバストテンソル分解
　5.5.3　ロバストテンソル分解の応用事例
章末問題

引用・参考文献
章末問題解答
索引

読者モニターレビュー【くりぽん様（業界・専門分野：教養学部情報コース）】

本書は、テンソルの定義とテンソルに関する計算から始まり、実装するためのプログラムを眺めながらテンソル分解とその応用を見ていく流れになっています。本書を読むにあたり前提知識は線形代数+αとなっておりますが、この「+α」の部分で読み進めるために最低限必要だと思われるのは、大学1, 2年で学ぶ微分積分、数理最適化問題と統計学の初歩的な知識かと思います。また、本書の特徴として、少ない前提知識から低ランク近似、テンソルデータ解析を理解することが可能となっている点や各項目において該当する内容を実装するためのアルゴリズムやソースコードが間に挟まっている点、ダイヤグラム表記をたくさん用いられている点が挙げられます。ここで、各章が何をしているのか簡潔に述べておきます。

第1章では、テンソルとはなにか？やテンソルの計算を視覚的に捉えるダイヤグラム表記、テンソルを使った表現の応用例（画像処理や関係データ、確率質量関数、回帰係数など）が紹介されています。
第2章では、各々のダイヤグラム表記とともにテンソルの変形や計算について書かれており、フロベニウスノルムや外積、カトリ・ラオ積などが挙げられております。
第3章では、線形代数の内容が書かれており、主に低ランク近似を行うための固有値分解や特異値分解について述べられています。また、主成分分析についても紹介されております。
第4章では、CP分解とTucker分解などのテンソル分解が紹介されています。ダイヤグラム表記を用いたテンソルトレイン分解が特徴的です。
第5章では、テンソル解析について紹介されています。

私は線形代数を学部1年のときに履修し、入門の教科書を数回読んだ程度の知識で読ませてもらいました。テンソルの計算を丁寧に紹介されていたので、第4章のテンソル分解までスムーズに理解することができました。また、ダイヤグラム表記がテンソル計算のときに、特に２つのテンソルもしくは行列の積においてどのモードについて合わせていくのかを視覚的に捉えられるのでとても役立ちました。しかし、私のようなレベル帯で一人で最後まで読むのは大変だと思います。第４章では、第２章で紹介されている複雑なテンソル計算をふんだんに用いているため、ダイヤグラム表記がありますが、細かい計算の部分は省力されているため追いかけるだけでも厳しいかと思います。また、ところどころ証明が省かれているので他の本で補うなどの処置が必要かもしれません。テンソルデータ解析について最低限の知識で理解したい、テンソル・線形代数の工学分野における応用例を見てみたい、実際にテンソルもしくはデータ解析の実装を行ってみたい、これら１つでも持っているならば本書を読み込むのは面白いかと思います。

読者モニターレビュー【 I.T. 様　大学院生（業界・専門分野：機械工学（振動工学・非線形力学・情報処理））】

テンソルやテンソル分解を基礎から応用まで日本語で丁寧に学べる貴重な書籍です。本書は、テンソルを理解するための導入として、配列（ベクトルや行列）の基本的な内容から始まり、線形代数の要点や主成分分析の解説を経て、テンソル分解やその応用についての方法論が詳細に説明されています。この流れにより、初心者でも段階的に理解を深めることができるよう配慮されています。
本書の特徴は、数式や数学表記が複雑になる部分に対しても、それぞれの概念や意味について大変丁寧な説明と豊富な図解が盛り込まれていることです。これにより、事前知識がほとんどない私でも挫折することなく理解を深めることができました。理論の説明に加えて、実装の手がかりとなるアルゴリズムやソースコード（MATLAB）も含まれているため、テンソル分解を実際に手で動かしてみる面白さも感じることができます。
また、本書はテンソルやテンソル分解の基礎から応用までを一冊で網羅しており、途中でわからない箇所があれば前半に戻って確認できるような構成になっています。多次元データの解析に関心がある方にとって、この書籍一冊でテンソルデータ解析を効率的に学べる最適な入門書であると感じました。

読者モニターレビュー【 charmie11 様　（業界・専門分野：Computer Vision）】

テンソル分解のアルゴリズムやテンソルデータ解析の応用の定式化を学びたい人におすすめします．
テンソル分解を含めたテンソルデータ解析の基礎理論について詳しくイメージ図を交えながら説明をしてくれており，何となく聞きかじったことのあるアルゴリズムが整理しやすいありがたい解説本という印象を受けました．特にテンソル分解について代表的な3アルゴリズムをわかりやすく解説してくれています．
強いて欠点を挙げるとすれば応用の説明が期待はずれでした．後半で解説しているテンソルデータ解析の応用例は問題・解法の定式化を丁寧にいている反面，具体的な応用例が少数しか掲載されていません．また，テンソル分解が目立たないような解説になっていて，頑張って理解したテンソル分解が...という気持ちになります．

読者モニターレビュー【大手希望様　（業界・専門分野：医用画像工学）】

本書はテンソルデータ解析の基礎と応用について、平易な語り口で述べたものです。テンソルの演算、線形代数の特異値分解を紹介した後、本書の肝となるテンソル分解について説明します。テンソル分解には、CP分解、タッカー分解、テンソルトレイン分解などがあり、本書を読むことによってそれらの違いを正確に理解することができます。また、応用として、ノイズ除去、補間、ボケ補正、超解像、フーリエ変換・ラドン変換に基づく画像再構成、圧縮センシングについて、コンパクトにまとめられています。ノイズ除去は、信号とノイズの2つの未知パラメータを1つの観測データから推定しなければならないため不良設定問題になるという説明はとてもわかりやすいです。交互方向乗数法、近接勾配法についてもまとめられており、ハイブリッドなデータ解析に興味のある読者にも有用な内容となっています。