科学技術と共に歩む

☆発行前情報のため，一部変更となる場合がございます

数理工学とは，数学の理論を基盤にして工学や情報科学の諸問題を解析し，その解決に役立つ新しい数理的手法を生み出すことを目的とする学問領域である。応用数学の一分野にとどまらず，工学的課題から新しい数学的概念や道具を引き出す点に大きな特徴がある。例えば，システム制御理論や最適化，信号処理やネットワーク解析，機械学習や暗号理論など，数理工学は現代の社会や技術に直結する幅広い分野で中心的な役割を担っている。

線形代数学は数理工学のあらゆる分野で基盤となる学問であり，行列演算や固有値問題，標準形などの理論が中心的な役割を果たしている。しかし，従来の教科書で展開される「体上のベクトル空間」を前提とした理論だけでは，整数環や多項式環を背景にした問題，データ解析や暗号といった現代的課題を十分に扱うことはできない。本書は，そうした背景のもとで，数理工学の多様な課題に通用する「広義の線形代数」を体系的に学べるように執筆したものである。読者が抽象的な線形代数学的視点と数理工学的視点を往復しながら学び進められるように，一冊の中で両者を結び付けることを目指している。

本書の大きな特徴は，ジョルダン標準形の位置付けを見直した点にある。従来の線形代数の教科書では，行列のジョルダン標準形の導出が学習の一つの到達点とされることが多い。しかし本書では，それを「広義の線形代数」の方法論を応用する題材と捉え直し，ユークリッド整域上のスミス標準形の理論を経由して体系的に導出する。こうすることで，複素数体上におけるジョルダン標準形が，より一般的な「ユークリッド整域を基盤にした加群や行列の分解理論」の特殊な姿として自然に現れることを明らかにし，標準形の理論を統一的に理解できるよう構成している。さらに，ジョルダン標準形の応用として，非負行列の理論とその応用を詳しく解説する。特に筆者自身の研究とも関わる，有向グラフに対応するグラフラプラシアンのクロン縮約については，その数理的性質と意義を詳細に論じる。

また，本書の「広義の線形代数」に含まれる代数学の考え方が多様な数理工学の問題において実際に役立つことを実感してもらうために，高速フーリエ変換（FFT）の理論も取り上げる。多項式の積を直接計算すると大きな手間がかかるが，「多項式を特定の点で評価し，その値を使って積をとり，最後にもとの形に戻す」という方法を利用すれば効率化できる。FFTはこの方法を再帰的に分解したアルゴリズムである。本書ではこの観点を通して，線形代数の考え方がどのように具体的なアルゴリズムと結び付き，数理工学に応用されていくのかを解説する。さらに，ジョルダン標準形導出の際に用いるスミス標準形が，トポロジカルデータ解析やシステム制御理論などの数理工学においてどのように応用されているかを簡潔に紹介した。

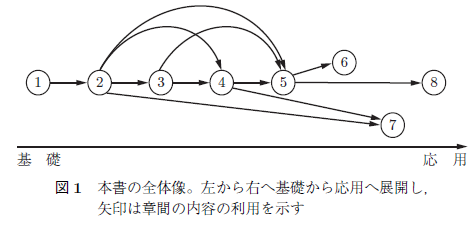
本書の構成はつぎのとおりであり，図1がその全体像である：第1章は集合・写像の基礎事項を整理し，さらに線形代数の教科書ではあまり扱われない商集合を導入する。商集合は抽象的な概念ではあるが，本書全体の理解において重要な役割を果たすため，特に丁寧に解説する。第2章では本書全体を通して中核となるユークリッド整域を中心に，代数学の基礎概念を詳述する。第3章では加群と準同型写像を取り上げ，ベクトル空間との違いを明確にしつつ，加群論の基本的枠組みを与える。第4章では整域上の行列式を定義から性質に至るまで体系的に構築し，後続の議論に備える。第5章ではエルミート標準形，スミス標準形，ジョルダン標準形という三つの標準形を取り上げ，特にジョルダン標準形と複素ベクトル空間の直和分解の関係を詳しく論じる。第6章では非負行列の一般論を展開し，その応用としてマルコフ連鎖を導入し，さらにグラフラプラシアンのクロン縮約について詳細に解説する。第7章では多項式の積とFFTの関係を線形代数学的観点から明らかにし，さらにFFTの深層学習モデルへの応用に触れる。最後に第8章では，本書で整えた「広義の線形代数」が具体的に数理工学のどのような分野に活用されるかを三つの視点から示す。すなわち，トポロジカルデータ解析，代数解析学に基づくシステム制御，そして耐量子暗号の有力候補である格子暗号である。