シリーズ刊行のことば
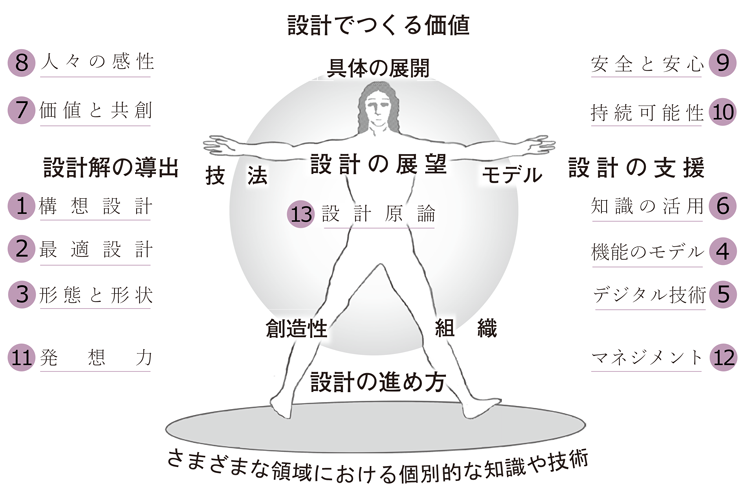
何とも,漠然とした閉塞感が漂う厄介な時代である。さらなる社会の発展や福祉の充実に向けて,研究開発の一層の充実が求められている一方で,その根幹である科学技術に20世紀のような青天井の輝きは乏しい。地球環境,経済の停滞や格差の拡大などの諸問題の解決に向けて,新たな科学技術が不可欠であることに疑う余地はないものの,それらの根源を探っていくと科学技術がもたらしたさまざまな手段に至って,つかみどころのない矛盾が顕わになる。今日の科学技術は,おおむね,17世紀に端を発するが,その中核をなした力学は,往時,さまざまなメカニズムが各種の機械に活用され始めた折,その設計を合理的に進めたいということが動機であったようである。対象を研ぎ澄まし論点を限定すると,その範囲内で繰り返される法則性が浮かび上がり,その法則性を明示的なものにすることにより,各種の設計は合理的で健全なものになってきた。研究開発とも呼応した産業活動が創り出す各種の人工物も大規模で複雑なものになってきて,想像もつかなかったような出来事が行きかうようにもなった。しかるに,今日のさまざまな問題は,どれ一つとして,固有の範囲内で生じているのではなく,多種多様な要因が折り重なって,厄介な問題となっている。となれば,そもそもの設計のありようが問われることになる。対象を限定せず,あくまでも広く横断的に見渡していくことを通じて,新たな機械,新たな人工物,今日的な意味合いでは,製品やサービスなどを創り出していく,そのような未来に向けた設計のあるべきすがたが問われている。
本「設計工学フロンティアシリーズ」は,上記のような問題意識のもと,社会や生活に関わる課題とさらに充実していく科学技術とを橋渡しし,健全な産業活動やそれを支える研究開発を描き出していくことを通じて,包括的な解決を導き出していく役割は新たな意味合いでの設計こそが担っていくとの考え方に立って,実用を旨とする工学の立場から,そのフロンティアを論じようとするものである。産業の実態にあっては,それぞれの専門に特化する分業が進み,大規模で複雑なバリューチェーンを通じて高度な人工物が創り出されるようになった。その背後では,入り組んだ因果関係のもと,新たなイノベーションを起こしていくことが一筋縄ではいかなくなっている。学術にあっても,この間の発展が積み重なってきた結果として,領域の細分化が相当に進んできている一方で,その弊害を克服するべく,学際融合の推進が希求されている。しかしながら,そのような学際融合も領域性を成立させてきた仕組みのもとにある。設計工学におけるフロンティアとは,そのような分業や領域性に起因する限界に対して,異なるレイヤーから,新たな実践なり学術を切り拓いていこうとするものとなる。
本シリーズでは,新たな地平に向けて,設計解を導き出すための考え方や方法論,設計を合理的かつ効率的に進めていくための支援技術,さらには,社会や生活における価値と相対する設計のあるべきすがた,設計の担い手となる人々や組織のあるべきすがたなどの各論について,それぞれに分冊を出版していくことを計画している。それぞれの分冊が,各方面での営みに新風を吹き込むこと,また,それに向けた学術が深まっていく足掛かりになっていくことを願っている。
2024年5月 編集委員長 藤田 喜久雄
編集委員会
編集委員長
編集委員(五十音順)
(所属は2024年5月現在)
シリーズラインナップ
以下続刊
- 構想設計の方法論(藤田喜久雄 著)
- 最適設計の基礎論(泉井一浩 著)
- 設計における形態と形状の創成(西脇眞二・竹澤晃弘 共著)
- 機能モデリングとモデルベース設計(梅田 靖・高本仁志 共著)
- デジタルエンジニアリングと設計(乾 正知・山﨑慎太郎・乙守正樹 共著)
- 設計における知識と管理(野間口 大・來村徳信 共著)
- 感性のモデリングと設計(柳澤秀吉・加藤健郎 共著)
- 安全と安心の設計論(小木曽 望 著)
- 持続可能システムの設計論―世界観とその展開―(小林英樹 著)
- 設計のための発想力(村上 存 著)
- 設計の組織化とマネジメント(青山和浩・古賀 毅 編著/江口隆夫・大泉和也 共著)
- 設計原論(藤田喜久雄 著)
設計工学フロンティアシリーズseries7
設計と価値の共創論 - 製品,サービス,そして人工物 -
- 下村芳樹 編著/赤坂文弥・根本裕太郎・三竹祐矢・筒井優介 共著
- A5サイズ/232頁
- 定価3,960円 (本体3,600円+税)
- ISBN 978-4-339-04707-3
価値の概念を中心として,関連する設計工学分野の動向を概観し,理念的設計への架橋とする

詳細へ
- 下村芳樹 編著/赤坂文弥・根本裕太郎・三竹祐矢・筒井優介 共著
- A5サイズ/232頁
- 定価3,960円 (本体3,600円+税)
- ISBN 978-4-339-04707-3
- 読者対象
- 価値とは何か?私たちはいかにその本質を知り,それを正しく満たし得るのか?本書は工学を起点としつつ,哲学を含む分野横断的な議論を展開し,社会のこの根源的な問いに対する一つの答えを提示します。ものとサービスの設計の思想,設計の戦略,設計の手法に興味と関心を有する工学分野に限らない幅広い読者を対象として想定しています。「広義の設計者」を目指す大学生や大学院生,企業の設計者,研究者,企画開発者,経営者だけでなく,自治体,公共団体における施策設計に携わる方,高校生や一般の方々など,様々な読者に価値の意味と設計の在り方を考えて頂くきっかけとなる内容となっています。
- 書籍の特徴
-
本書では,価値という誰もがそれを重要であると認識しつつ,その実態を理解しづらい概念を務めて簡潔に再定義することを試みました。ものとサービスの設計を介して,私たちはいかに価値を知り得るのか?いかに満たし得るのか? この問いに対して,過度に専門的で難解な説明に陥らないように,一般的な用語で分かり易く説明し,より多くの方々に関連する問題の重要性を知って頂き,今後の議論と設計に参加する意識を持って頂くことを目指しました。価値を充足するという目的のもとで,社会で極めて広く,誰もが行う一般的な思考であるにも関わらず,ややもすれば工学やものづくりの限られた領域に閉じて議論されがちである設計という概念を,意味,意義,成り立ち,手法,そしてそこに生じた新しい変化と今後の方向性という複数の観点から,事例を交えて横断的,網羅的かつ簡潔に紹介しています。価値と設計の本質を知る入門書として利用して頂くほか,永らく手元に置いて字引的にも活用して頂けるように資料的価値も高まるように努めました。
【各章について】
1章では,本書における導入の章としての位置づけのもとで,人工物の定義と歴史,存在意義を振り返り,設計と呼ばれる人の創造行為が果たした意味を再考します。
2章では,現代社会において価値は創り出すものであること,価値の創造と提供に共感が果たす役割を解説しながら,今後の設計の方向性を示す理念的設計(プラトニックデザイン)の思想を紹介します。
3章では,過去から現在にいたる価値概念の系譜を俯瞰します。さらに近年の価値観における象徴的な概念を紹介し,それらが登場した社会的な背景を解説します。
4章では,科学と工学に古くより存在する関係,新たに生じつつある関係を論考します。さらに,人の思考の類型の観点で設計の過程を整理します。
5章では,誤り得る推論,限定合理性という人の限界がもたらす可能性を論考します。アブダクション・創造・共感の関係について解説します。
6章では,サービス化が製造業を中心とする実業にもたらした影響と,そこに浸透しつつあるサービス設計の手法を紹介します。
7章では,共創的な設計の実際を紹介します。社会的な価値と影響を考慮した設計,人間中心設計,参加型デザイン,リビングラボなどの取り組みを参照しながら,社会の要求に応えるために生じた設計の変化を概説します。
8章では,社会と人工物の間に生じる共進化と呼ばれる関係を再考し,人工物の社会実装に関する課題を整理します。
9章では,時間と価値の関係を議論します。時間軸上で価値を設計する試みに寄せられている社会の期待について解説します。
10章は,本書の終章として,「設計工学のフロンティア」を素描します。設計の発展に寄与すると期待される関連領域を予想し,価値を中心とする設計の将来像を提示します。 - 目次
-
1. 設計と創造
1.1 製品,サービス,そして人工物
1.2 人工物と設計
1.2.1 19世紀の人工物
1.2.2 20世紀の人工物
1.2.3 21世紀の人工物
1.2.4 人工物発展の軌跡
2. 社会問題と設計
2.1 社会問題と創造
2.2 社会問題の深因と日本の固有性
2.3 イデオロギーの背景
2.4 memento moriの戒告
2.5 理念的設計(プラトニックデザイン)の思想
3. 価値の変遷
3.1 設計と価値
3.2 新しい価値観
3.3 工学における価値
3.4 価値共創
4. 設計の形態
4.1 工学と設計
4.2 工学設計の形態
4.2.1 Asimowの工学設計
4.2.2 Archerのシステマティックモデル
4.2.3 PahlとBeitzの製品開発プロセス
4.2.4 最適設計
4.3 設計の論理
4.4 一般設計学の世界
5. 設計とabduction
5.1 なぜ価値創造か
5.2 合理性の限界
5.2.1 Condillacの思想
5.2.2 Wittgensteinの言語ゲーム
5.2.3 限定合理性
5.3 創造とabduction
5.4 イノベーションとabduction
5.5 創造性の涵養方法
5.5.1 ブレインストーミング
5.5.2 KJ法,親和図法
5.5.3 TRIZ
5.5.4 SECIモデル
5.5.5 serious play
5.6 創造的設計の支援の試み
6. サービスの価値と設計
6.1 社会におけるサービス化の進展
6.1.1 製造業のサービス化
6.1.2 サービス化の効果
6.1.3 デジタル化によるサービスの進展
6.2 サービスの理論
6.2.1 サービスの捉え方
6.2.2 サービス・ドミナント・ロジック
6.2.3 使用価値
6.3 サービスの設計
6.3.1 サービス工学
6.3.2 サービス設計学
6.3.3 サービスデザイン
6.4 デジタルテクノロジーとサービス
6.4.1 スマートなサービス
6.4.2 スマートなサービスの設計
7. 共創の設計論
7.1 共創的なデザインアプローチ
7.2 人間中心設計
7.2.1 HCDとUX
7.2.2 HCDのプロセス
7.3 参加型デザイン/CoDesign
7.3.1 参加型デザイン
7.3.2 CoDesign
7.4 共創のための手法
7.4.1 フォーカスグループ
7.4.2 generative design tool
7.4.3 スキット
7.5 パタン・ランゲージ
7.5.1 パタン・ランゲージとは
7.5.2 パタン・ランゲージの活用方法
7.6 リビングラボ
7.6.1 リビングラボとは
7.6.2 リビングラボのタイプ
7.6.3 オープンデザインとリビングラボ
7.6.4 リビングラボの進め方
7.6.5 リビングラボ実践のノウハウ
8. システムと設計
8.1 システムとは何か
8.2 さまざまなシステム概念
8.2.1 社会技術システム
8.2.2 製品サービスシステム
8.2.3 サイバーフィジカルシステム
8.3 システムの多層的フレームワーク
8.3.1 システム・アーキテクチャ
8.3.2 マルチレベルデザイン
8.4 システムのデザインアプローチ
8.4.1 システムズ・エンジニアリング
8.4.2 ソフト・システムズ・アプローチ
8.4.3 システム・ダイナミクス
8.5 社会的影響とデザイン
9. 価値と時間軸
9.1 価値と時間
9.2 時間の性質
9.2.1 不可止性と不可逆性
9.2.2 普遍性と唯一性
9.2.3 確実性と不確実性
9.3 時間と変化
9.3.1 時間とスケール
9.3.2 意図に基づく変化の分類
9.3.3 文脈の時間変化
9.4 時間軸のマネジメント
9.4.1 シナリオ・プランニング
9.4.2 トランジション・マネジメント
9.5 時間軸の設計方法論
9.5.1 アップグレード設計
9.5.2 UXデザイン
9.5.3 価値成長デザイン
9.5.4 PSSのタイムアクシス・デザイン
9.5.5 デザイン・フィクション
9.5.6 トランジション・デザイン
9.6 時間軸設計への期待
10. 価値設計のフロンティア
10.1 理念的設計(プラトニックデザイン)の実現に向けて
10.2 理念的設計のプロセス規範
10.2.1 人工物を共創する―二つのレベル―
10.2.2 設計のスコープを動かす―外部要因の包摂―
10.2.3 インパクトを継続的に評価する―プロジェクトからプロセスへ―
10.3 工学的設計の可能性
10.3.1 プロセス化の視点
10.3.2 モデル化の視点
10.3.3 知能化の視点
引用・参考文献
あとがき
索引more - 著者からのメッセージ
- 科学の本質は,事象の真実を明らかにし,その結果を整理し体系化することです。他方,自然には存在しない人工物を産み出すことはこれとは異なり,誤り得ることを認める,設計という思考により為されます。設計の目的は,事象を明らかにすることではなく,事象を実現することにあるのです。結果として,科学性を重視する工学教育の場では,この意味に沿う設計の教育は整備も提供も十分にされていないのです。主観に基づく「価値」の話題が工学から遠ざけられ,避けられて来た理由もここにあります。設計において,本来は最も重要であるはずの,なぜつくるのか,何をつくるべきか,何をつくらざるべきかを明らかにする知は,工学はおろか設計に関係する学際においても正面から扱われることは殆ど無かったのです。そしてこの大きな矛盾は,工学と社会の間に大きな乖離を招いています。本書はこの矛盾の存在とその解決の重要性を先ず工学の立場から指摘し,この議論が社会に広がることを願って執筆しました。本書の書名はダブルミーニングになっており,一つは「設計」と「価値の共創」の関係を論じること,一つは,「設計と価値」の「共創」を論じることです。本書を通じて,より多くの方にこれらに係る議論に参画して頂くことを願っています。
- キーワード
- 価値,設計,共創,共感,アブダクション,プラグマティズム,イノベーション,サービス化,サービス工学,設計論,設計方法論,理念的設計
設計工学フロンティアシリーズseries1
構想設計の方法論
- 藤田喜久雄 著
機械学習の基本タスクである回帰と識別のための様々な手法について,その本質と特性を解説
- 読者対象
- 機械学習,パターン認識,ニューラルネットなどに興味を持っている学生,研究者
- 書籍の特徴
-
本書は,パターン認識において用いられる線形回帰や線形判別分析といった手法について,「各手法が本質的になにを実現しようとしているのか」という点を理解するうえで一つの答えを示しています。パターン認識をこれから新たに学びたいと考えている読者はもちろん,各手法をもう少し統一的に理解がしたいと思っている読者にとっても気づきが得られる内容です。
本質的な理解のアプローチとして,機械学習の最も基本的なタスクである回帰と識別について最適な非線形関数がなにかを知り,パターン認識で使われる各手法がその最適な非線形関数をどのように近似しているのかを理解できるような構成となっています。この点はほかの書籍にはみられないアプローチです。
パターン認識をこれから新たに学びたいと考えている読者はもちろん,各手法をもう少し統一的に理解がしたいと思っている読者にとっても気づきが得られるはずです。【各章について】
各章での説明の流れを簡単に説明します。
はじめの1,2章でベイズ識別の仮定と同様に,訓練サンプルが無限にあり,データの背後の確率的な関係が完全にわかっている場合について,変分法を用いて予測や識別のための最適な非線形関数を導出します。これにより,訓練用のデータ(訓練データ)から学習したモデルが究極的になにを学習しているかを理解します。
(ベイズ識別の理論では,対象の観測値とクラスとの確率的な関係が完全にわかっているという仮定のもとで,識別誤りを最小とする最適な方式が事後確率が最大のクラスの識別方式となることが知られています。)
しかし,実際の応用データでは,データの背後の確率的構造がわかっていることはまれで,それらを訓練データから推定する必要があります。訓練データから確率分布を推定することができれば,推定結果を利用して予測のための最適な非線形関数を近似するモデルを求めることができます。この点について3章で解説しています。
つづく4章では,確率分布の推定を経由せずに,訓練データから直接,入力ベクトルから目的変数の値を推定する関数を構成する手法(線形回帰分析)を解説。さらに5章で,同様にして訓練データから直接,入力ベクトルからクラスを推定する線形識別関数を求める手法として
- 2クラス識別のための線形モデル:単純パーセプトロン,ADALINE,ロジスティック回帰,サポートベクトルマシン
- 多クラス識別のための線形モデル:最小二乗線形識別関数,多項ロジスティック回帰
- 線形識別関数の学習のためのモデルを層状に結合した,多層パーセプトロン
6章では,主成分分析と線形判別分析について,それぞれ手法の特徴と訓練データとの関係に触れたうえで解説を行い,本質的な理解を目指します。
7章では, 特徴ベクトルを非線形に変換することで,その空間で線形モデルを用いて予測や識別を行う手法であるカーネル法について解説します。この方法を用いることでサポートベクトルマシンの認識性能が飛躍的に向上しましたが,本書籍で扱ったほかの多くの線形手法を非線形に拡張する場合にも利用できます。本章ではカーネル回帰,カーネルサポートベクトルマシン,カーネル主成分分析,カーネル判別分析を詳しく採り上げます。
最後の8章では,訓練サンプルが無限にあり,データの背後の確率的な関係がわかっていると仮定して,判別基準を最大とする最適な非線形判別関数を用いて導出する(大津展之先生による手法)。さらに,導出した最適な非線形判別写像と線形判別分析との関係について議論し,カーネル法を別の視点から眺めてみることで,導出した最適な非線形判別分析写像から最適なカーネル関数の導出を行います(判別カーネル)。 - 目次
-
1. パターン認識とベイズ決定理論
1.1 パターン認識
1.2 ベイズ決定理論
1.2.1 特徴ベクトルとクラスとの確率的関係
1.2.2 ベイズ決定理論の定式化
1.2.3 0-1損失の場合
1.3 正規分布の場合のベイズ識別
1.3.1 二次識別関数
1.3.2 線形識別関数
1.3.3 テンプレートマッチング
1.3.4 Fisherのアヤメのデータのベイズ識別
2. 最適な回帰と識別
2.1 機械学習
2.2 予測のための最適非線形回帰
2.2.1 平均二乗誤差を最小とする最適な非線形関数の導出
2.2.2 非線形回帰関数fopt(x)の最適性
2.2.3 最適な非線形回帰関数fopt(x)で達成される誤差
2.2.4 最適な非線形回帰関数の統計量
2.3 識別のための最小二乗非線形関数
2.3.1 識別のための非線形関数を構成する方法
2.3.2 識別のための最適な非線形回帰関数で達成される平均二乗誤差
2.4 識別のための非線形識別関数
2.4.1 2クラス識別の場合
2.4.2 Kクラスの場合
3. 確率分布の推定
3.1 確率分布の推定法
3.2 パラメトリックモデルによる確率分布の推定
3.2.1 最尤法
3.2.2 最尤法による確率密度関数の推定の応用
3.3 ノンパラメトリックモデルを用いる方法
3.3.1 ノンパラメトリックな確率密度関数の推定
3.3.2 核関数に基づく方法
3.3.3 K-最近傍法
3.3.4 K-最近傍法による確率分布の推定の応用
3.4 セミパラメトリックな手法
3.4.1 混合分布モデル
3.4.2 混合分布モデルのパラメータの最尤推定
3.4.3 EMアルゴリスム
3.4.4 混合分布モデルによる確率密度関数の推定の応用
4. 予測のための線形モデル
4.1 線形回帰分析
4.1.1 線形回帰分析のモデル
4.1.2 最小二乗法
4.1.3 最適な線形回帰関数flinreg(x)で達成される平均二乗誤差
4.1.4 最適な線形回帰関数の統計量
4.1.5 線形回帰分析の応用
4.2 最適な非線形回帰関数との関係
4.2.1 予測のための最適な線形回帰関数
4.2.2 最適非線形回帰関数の線形近似
4.2.3 条件付き確率の線形近似
4.2.4 条件付き確率の線形近似による最適な非線形回帰関数の近似
4.3 線形モデルを用いた非線形回帰
4.3.1 多項式回帰
4.3.2 基底関数の線形モデルによる回帰
4.3.3 回帰式のカーネル関数による表現
4.4 回帰分析と汎化性能
4.4.1 多項式回帰と汎化性能
4.4.2 モデルの良さの評価
4.5 正則化回帰
4.5.1 リッジ回帰
4.5.2 L1正則化回帰(lasso)
5. 識別のための線形モデル
5.1 線形識別関数とその性質
5.1.1 線形識別関数
5.1.2 線形識別関数の性質
5.1.3 線形分離可能
5.2 単純パーセプトロン
5.2.1 単純パーセプトロンのモデル
5.2.2 単純パーセプトロンの学習
5.2.3 アヤメのデータの単純パーセプトロンでの識別
5.3 Adaptive Linear Neuron(ADALINE)
5.3.1 ADALINEのモデル
5.3.2 ADALINEの学習
5.3.3 回帰分析との関係
5.3.4 正則化ADALINE
5.3.5 アヤメのデータのADALINEでの識別
5.4 ロジスティック回帰
5.4.1 ロジスティック回帰のモデル
5.4.2 ロジスティック回帰のパラメータの学習
5.4.3 Fisher情報行列を用いる学習法
5.4.4 正則化ロジスティック回帰
5.4.5 アヤメのデータのロジスティック回帰での識別
5.5 サポートベクトルマシン
5.5.1 サポートベクトルマシンのモデル
5.5.2 線形分離可能な場合のパラメータの学習
5.5.3 線形分離可能でない場合のパラメータの学習
5.5.4 サポートベクトルマシンとロジスティック回帰
5.5.5 アヤメのデータの線形サポートベクトルマシンでの識別
5.6 多クラス識別のための線形識別関数の学習
5.6.1 多クラス識別のための線形モデル
5.6.2 最小二乗線形識別関数
5.6.3 多項ロジスティック回帰
5.6.4 アヤメのデータの多クラス識別
5.7 識別のための最適な非線形関数との関係
5.7.1 識別のための最適な線形関数
5.7.2 事後確率の線形近似
5.8 多層パーセプトロン
5.8.1 多層パーセプトロンのモデル
5.8.2 多層パーセプトロンの能力
5.8.3 誤差逆伝播学習法
5.8.4 畳込みニューラルネットワーク(CNN)
6. 主成分分析と判別分析
6.1 主成分分析
6.1.1 主成分分析の問題設定
6.1.2 第一主成分の導出
6.1.3 第二主成分の導出
6.1.4 高次の主成分の導出
6.1.5 寄与率と累積寄与率
6.1.6 主成分分析の適用例
6.1.7 元のデータの再構成
6.1.8 主成分スコアベクトル間の距離
6.2 線形判別分析
6.2.1 一次元の判別特徴の抽出
6.2.2 多次元の判別特徴の構成
6.2.3 2段階写像としての判別写像
6.2.4 判別特徴ベクトル間の距離
6.2.5 線形判別分析の適用例
7. カーネル法
7.1 カーネル法とは
7.2 カーネル回帰分析
7.2.1 カーネル回帰分析とは
7.2.2 カーネル法を用いた最小二乗識別関数の学習
7.3 カーネルサポートベクトルマシン
7.3.1 カーネルサポートベクトルマシンとは
7.3.2 最適なハイパーパラメータの探索
7.4 カーネル主成分分析
7.5 カーネル判別分析
7.5.1 カーネル判別分析とは
7.5.2 カーネル判別分析の適用例
8. 最適非線形判別分析と判別カーネル
8.1 最適非線形判別写像
8.1.1 最適非線形判別写像の導出
8.1.2 事後確率ベクトルの線形判別分析
8.1.3 最適非線形判別写像の線形近似
8.2 事後確率の近似を通した非線形判別分析
8.2.1 正規分布を仮定することによる非線形判別分析
8.2.2 K-最近傍法を用いた非線形判別分析
8.2.3 ロジスティック回帰に基づく非線形判別分析
8.2.4 非線形判別空間の比較
8.3 判別カーネル
8.3.1 最適非線形判別分析の双対問題
8.3.2 有効なカーネルの条件
8.3.3 判別カーネルと周辺化カーネルの関係
8.3.4 判別カーネルの族
付録
A.1 線形代数のまとめ
A.2 ベクトル・行列の微分と最適化の基礎
A.3 確率統計の基礎
引用・参考文献
あとがき
索引more - 著者からのメッセージ
-
パターン認識・機械学習分野の中で「回帰」と「識別」を中心に取り扱う本ですが,従来の類書では詳しく書かれていないであろう式展開なども多く盛り込んでいます。
特に「変分法」や「ベイズ事後確率の線形近似」という道具立てで回帰分析と判別分析の知られざる素性や性質を詳らかにしている部分などをお楽しみ頂ければと思います。 - キーワード
- パターン認識,機械学習,線形判別分析,カーネル判別分析,最適非線形判別分析,判別カーネル,線形回帰,ロジスティック回帰,カーネル回帰,最適非線形回帰,ベイズ決定理論,事後確率,変分法,サポートベクトルマシン,主成分分析,カーネル法,周辺化カーネル
設計工学フロンティアシリーズseries2
最適設計の基礎論
- 泉井一浩 著
ボルツマンマシンの基本的な理論から学習方法、そして機械学習や強化学習への用い方について直観的に理解できるよう解説。
- 読者対象
- 学部生が読めるレベルを心がけています。ボルツマンマシンを通じて機械学習・強化学習に必要な基礎的な知識が身に着けられます。一方で,網羅的ではありませんが,ボルツマンマシンに関する幅広い話題を取り上げているので,ボルツマンマシンや関連分野の研究者が読んでも新たな気付きが得られることを期待しています。
- 書籍の特徴
-
ボルツマンマシンという一つの確率モデルに限定して、機械学習・強化学習への幅広い適用方法について説明しています。ボルツマンマシン以外のモデルを機械学習・強化学習に用いる際にも有用な、確率的勾配法や強化学習の基礎について特に丁寧に説明しています。
【各章について】
各章での説明の流れを簡単に説明します。
1章では,「ボルツマンマシンとはなにか」,「学習するとはどういうことか」,「学習によってなにができるようになるのか」をテーマとして解説を行います。また,ボルツマンマシンは,「勾配法」や「確率的勾配法」を適用して学習することが多いので,これらの基礎についての確認も行います。
2章では,ボルツマンマシンを勾配法で学習する際に必要となる勾配や,勾配法に有用な情報を与えるヘッセ行列を具体的に導出します。なお,ボルツマンマシンの学習は一般には計算量的に困難であるため,何かしらの近似をするか,ボルツマンマシンの構造を限定する必要があります。この計算困難さを克服する「制限ボルツマンマシン」について,本章で解説します。
3章では,ボルツマンマシンが定める確率分布の期待値を近似的に評価します。ボルツマンマシンは確率分布を定めますが,この確率分布に関する期待値の評価が学習に必要となります。ただし,一般にはこの期待値を閉形式で書くことはできず,期待値を厳密に評価するのは計算量的に困難であるため,ここでは近似的に評価を行います。また,制限ボルツマンマシンが持つ構造を利用すると,近似に必要な計算を効率的に行えるようになることについても確認します。
ボルツマンマシンと関連する代表的な深層ニューラルネットワークに「深層信念ネットワーク」と「深層ボルツマンマシン」があり,これらのニューラルネットワークは多数の層からなります。4章では,これらについて,制限ボルツマンマシンを用いて層ごとに学習していく手法を解説します。これは深層学習が注目されるきっかけとなった手法です。
5章ではボルツマンマシンを用いた時系列モデルの解説を行います。ボルツマンマシンの構造を工夫すると,複数のパターンが時間の順番に並んだ時系列データを学習して,将来の値の予測などに使えるようになります。
時系列データは順番に観測されていきますが,データが生成される環境が時間とともに変化する場合には,その変化に合わせて時系列モデルを更新していく必要があります。6章では,各時点で観測されるパターンに基づいて,モデルのパラメータを逐次的に更新するオンライン学習について解説します。このオンライン学習を効率的に行うのが「動的ボルツマンマシン」です。
7章ではボルツマンマシンがどのように強化学習に使えるのかを解説します。強化学習では候補となる行動の数が多いと効率的な使用が難しくなりますが,ボルツマンマシンを用いることでこの難しさが解消されます。強化学習の基礎となるマルコフ決定過程から説明を始め,ボルツマシンを強化学習に適用していきます。強化学習の基礎的な内容も学べます。 - 目次
-
1. はじめに
1.1 ボルツマンマシンと深層学習
1.2 ボルツマンマシンの定義
1.3 ボルツマンマシンの可能性
1.4 学習の目的関数
1.5 勾配法
1.6 確率的勾配法
章末問題
2. ボルツマンマシンの学習
2.1 可視ユニットのみの場合
2.1.1 勾配
2.1.2 確率的勾配
2.1.3 ヘブ則との関係
2.1.4 ヘッセ行列
2.1.5 まとめ
2.2 隠れユニットを持つ場合
2.2.1 隠れユニットの必要性
2.2.2 自由エネルギー
2.2.3 勾配
2.2.4 確率的勾配
2.2.5 ヘッセ行列
2.2.6 まとめ
2.3 判別モデルの学習
2.3.1 目的関数
2.3.2 勾配とヘッセ行列
2.3.3 まとめ
2.4 回帰モデルの学習
2.4.1 自由エネルギーを用いた回帰
2.4.2 制限ボルツマンマシンの自由エネルギー
2.4.3 期待エネルギー
2.4.4 期待エネルギーを用いた回帰
章末問題
3. サンプリングと期待値の評価
3.1 ギブスサンプリング
3.2 コントラスティブダイバージェンス
3.3 制限ボルツマンマシンからのサンプリング
3.3.1 ブロック化ギブスサンプラー
3.3.2 生成モデルの学習
3.4 平均場近似
3.5 その他の手法
3.5.1 重点サンプリング
3.5.2 独立した生成器の利用
3.5.3 フィッシャーダイバージェンス
章末問題
4. 深層モデルとその他の関連するモデル
4.1 深層信念ネットワーク
4.1.1 確率分布とサンプリング
4.1.2 層ごとの貪欲学習法
4.1.3 自己符号化器
4.2 深層ボルツマンマシン
4.3 ガウスボルツマンマシン
4.3.1 期待値で実数値を表現する場合の問題点
4.3.2 ガウスベルヌーイ制限ボルツマンマシン
4.3.3 スパイクスラブ制限ボルツマンマシン
4.4 マルコフ確率場
4.4.1 ボルツマンマシンとイジングモデル
4.4.2 高階ボルツマンマシン
章末問題
5. 時系列モデルの学習
5.1 目的関数と勾配法
5.2 条件付き制限ボルツマンマシン
5.2.1 条件付き制限ボルツマンマシンの導出
5.2.2 条件付き制限ボルツマンマシンの拡張
5.3 再帰的時間的制限ボルツマンマシン
5.3.1 時間的制限ボルツマンマシン
5.3.2 再帰的時間的制限ボルツマンマシンの導出
5.3.3 再帰的時間的制限ボルツマンマシンにおける確率の評価
5.3.4 再帰的時間的制限ボルツマンマシンの学習
章末問題
6. 時系列モデルのオンライン学習
6.1 はじめに
6.2 動的ボルツマンマシン
6.2.1 有限動的ボルツマンマシン
6.2.2 動的ボルツマンマシンの導出
6.2.3 スパイク時間依存可塑性との関係
6.3 制約の緩和
6.4 連続値をとる時系列に対する動的ボルツマンマシン
6.4.1 ガウス動的ボルツマンマシン
6.4.2 自然勾配
6.4.3 非線形特徴量
6.5 動的ボルツマンマシンの連続拡張
章末問題
7. 強化学習
7.1 マルコフ決定過程
7.2 最適性方程式と価値反復法
7.2.1 有限期間の場合
7.2.2 無限期間の場合
7.3 Q学習
7.4 活用と探索
7.5 SARSA法
7.6 方策反復法
7.7 価値関数の近似
7.7.1 Q学習での関数近似
7.7.2 SARSA法での関数近似
7.8 自由エネルギーを用いた強化学習
7.8.1 自由エネルギーの勾配
7.8.2 ボルツマン探索
7.9 部分観測環境における強化学習
7.9.1 部分観測マルコフ決定過程
7.9.2 動的ボルツマンマシンによる強化学習
章末問題
付録:隠れユニットを持つ動的ボルツマンマシン
A.1 確率分布
A.2 学習則
引用・参考文献
章末問題解答
索引more - 著者からのメッセージ
- できるだけ直感的な理解が得られるように説明を工夫しました。これまで分からなかったことが「分かった」「なるほど」と思っていただける箇所があれば幸いです。
- キーワード
- ボルツマンマシン,制限ボルツマンマシン,動的ボルツマンマシン,ニューラルネットワーク,深層ネットワーク,深層学習,機械学習,強化学習,表現学習,深層強化学習,コントラスティブダイバージェンス,確率的勾配法,自由エネルギー,生成モデル,時系列,Q学習,SARSA
設計工学フロンティアシリーズseries3
設計における形態と形状の創成
- 西脇眞二・竹澤晃弘 共著
捜索理論について,初学者でも学べるように確率論や最適化理論,ゲーム理論などの捜索理論を理解するために必要な基礎理論から解説。
- 読者対象
- 本格的に捜索理論(または探索理論)を学びたいと思っている学生や研究者はもとより,「私達の身の回りに見出だせる問題を数理的に分析したい」と考えている読者も対象としています。これは,捜索理論がそのような分析手法の体系をもつオペレーションズ・リサーチ(OR)の一分野として発展したものであるため,実世界における意思決定問題への理論の具体的な適用手順を習得できるからです。
- 書籍の特徴
-
7章と10章では,数理的分析には欠かせない一般理論である「最適化理論」(線形計画法,非線形計画法,動的計画法及び変分法)と「ゲーム理論」の重要な定理や理論について,役立つことや応用を第一義として書いています。そのため,これらの理論に興味のある学生が,捜索理論に関連するその他の章をスルーして,7章と10章だけを読んでいただいても,理論の核となる部分を端的に学ぶことができます。
私達を取り巻く実世界には様々な意思決定場面があり,その問題を解くためには,まずはそれを記述・定義して,自分の目前に明示するところから始めなければいけません。それができれば,後は上記のような一般理論の大海の中でこれまで開発され蓄積されてきた解法が利用できるかもしれません。このような問題の記述・定義の作法についても,本書により学ぶことができます。
以上は,これまで出版された捜索理論(探索理論)関係の本とは異なる本書の特徴でもあります。 - 目次
-
1. はじめに
2. 確率論
2.1 集合と事象
2.1.1 集合
2.1.2 写像
2.1.3 事象と確率
2.2 条件付き確率
2.2.1 条件付き確率とは
2.2.2 ベイズの定理
2.3 確率変数
2.3.1 離散確率変数と連続確率変数
2.3.2 離散確率変数と連続確率変数の例
2.3.3 確率変数に関する特性値・期待値・分散
2.4 二次元平面上の確率計算
章末問題
3. 目標存在分布の推定
3.1 方位線情報による目標分布推定
3.1.1 多角形による推定
3.1.2 最尤推定による推定
3.2 定針・定速の拡散目標の分布推定
3.2.1 デイタム位置が確実な場合の目標分布
3.2.2 デイタム位置が不確実な場合の目標分布
3.3 ランダムウォーク移動目標の分布推定
3.4 スコーピオン号事件と捜索救難の発展
3.5 捜索実施結果を加味した目標存在の事後推定
3.5.1 目標存在分布の更新
3.5.2 重み付けシナリオ法による目標分布の推定
章末問題
4. 捜索センサーの探知論
4.1 捜索センサーの瞬間的な探知能力
4.2 目標移動におけるセンサーの探知能力
4.2.1 探知ポテンシャル
4.2.2 横距離探知確率と有効捜索幅
4.3 ビークルの捜索能力
章末問題
5. 静止目標に対する捜索モデルとその評価
5.1 区域捜索のモデル
5.1.1 平行捜索
5.1.2 ランダム捜索
5.1.3 区域捜索法の比較
5.2 デイタム捜索のモデル
5.2.1 規則的なデイタム捜索
5.2.2 ランダム・デイタム捜索
5.2.3 デイタム捜索法の比較
章末問題
6. 移動目標に対する捜索モデルとその評価
6.1 区域捜索と動的増分係数
6.2 移動目標と捜索者の会的
6.2.1 近接可能領域
6.2.2 探知方位の分布
6.3 デイタム捜索
6.3.1 定針・定速目標に対するデイタム捜索
6.3.2 ランダムウォーク目標に対するデイタム捜索
6.4 バリヤー哨戒
6.4.1 8の字哨戒
6.4.2 往復哨戒
6.4.3 8の字哨戒と往復哨戒の比較
章末問題
7. 最適化理論
7.1 線形計画法
7.1.1 線形計画問題による定式化
7.1.2 双対理論
7.2 非線形計画法
7.2.1 制約条件のない最適化問題
7.2.2 等式制約をもつ最適化問題とラグランジュの未定乗数法
7.2.3 不等式制約をもつ最適化問題とKarush-Kuhn-Tucker条件
7.3 動的計画法
7.3.1 最適性の原理
7.3.2 動的計画法による定式化とさまざまな最適政策
7.4 変分法
7.4.1 オイラー方程式
7.4.2 オイラー・ラグランジュ方程式の拡張
章末問題
8. 静止目標に対する最適資源配分
8.1 クープマン問題
8.2 その他の評価尺度の最適捜索
8.2.1 生存探知確率
8.2.2 期待利得
章末問題
9. 移動目標に対する最適資源配分
9.1 探知確率最大化問題
9.1.1 マルコフ移動目標に対する最適資源配分
9.1.2 パス型移動目標に対する最適資源配分
9.2 期待利得最大化問題
9.3 捜索経路の制約付き捜索問題
10. ゲーム理論
10.1 問題のゲームによる表現
10.2 2人ゼロ和ゲームと均衡解
10.2.1 鞍点
10.2.2 支配戦略
10.2.3 連続ゲーム
10.2.4 混合戦略と均衡解
10.2.5 ミニマックス定理と最適混合戦略の求め方
10.3 非ゼロ和ゲームとナッシュ均衡解
10.4 展開形ゲーム表現と多段ゲーム
10.4.1 展開形ゲームの定義
10.4.2 展開形ゲームにおける戦略と行動戦略
10.4.3 確率ゲーム
10.5 情報不完備ゲームとベイジアンゲーム
章末問題
11. 捜索ゲーム
11.1 静止目標に関する捜索ゲーム
11.2 移動目標に関する捜索ゲーム
11.2.1 目標のパス型移動を用いた均衡解
11.2.2 目標のマルコフ移動を用いた均衡解
11.3 捜索ゲームに関するその他のモデル
11.3.1 虚探知の発生する捜索
11.3.2 多段階の捜索ゲーム
11.3.3 目標の初期位置が個人情報である情報不完備捜索ゲーム
章末問題
参考文献
索引more - 著者からのメッセージ
-
最後に,捜索理論を学ぼうとする方に,捜索理論は何の役に立つのかを伝えるべきでしょうが,捜索理論を学ぼうと考えた時点で,これを何に使おうかという腹案はお持ちかと思います。なぜなら,捜索理論そのものはORの分野でもマイナーであり,あえてこの分野を探し当てた方は,何かしらの特別な意図をお持ちかと思うからです。したがって,本書の「まえがき」や「はじめに」の章や目次に目を通していただき,捜索理論が役立つ具体的な問題の草案を練っていただきたく思います。
2019年初頭にあたって,捜索理論の主要テーマの領域外にも,日本が直面している災害対策や防衛問題,小さなテーマで言えば,無人航空機やドローンの効果的な活用などには,捜索理論に対する時代のニーズがあるようにも思えます。 - キーワード
- オペレーションズ・リサーチ,センサー,探知,哨戒,監視,捜索救難,レーダー,音響センサー,ソノブイ,数理計画法,最適化理論,線形計画法,非線形計画法,動的計画法,変分法,確率論,ゲーム理論,探知確率,存在分布,ランダムウォーク,ソリューション,デイタム捜索,区域捜索,バリヤー哨戒
設計工学フロンティアシリーズseries4
機能モデリングとモデルベース設計
- 梅田 靖・高本仁志 共著
本書では,現在の状況を表す状態を観測しながら,ある利益(費用)規範の下で最適な決定を行う確率過程であるマルコフ決定過程の基本理論や実際に問題を定式化して解き,最適決定政策を求める際必要となる計算手法に焦点をあて解説した。
- 読者対象
- マルコフ決定過程について基礎から学びたい学生・研究者を読者として想定しています。オペレーションズ・リサーチの研究に従事し,確率的な要素を含む動的最適化問題における最適決定政策を導出する方法に興味がある方,ならびに情報分野で強化学習について学ぶ際その基礎となるマルコフ決定過程について理解したい方などが対象となります。
- 書籍の特徴
-
この本のみでマルコフ決定過程の理論を学べるように,基礎となる動的計画法,確率変数,確率過程について詳しく述べています。その上で,マルコフ決定過程の各種最適化規範について,基本的かつ重要な理論と,最適決定を求めるアルゴリズムについて詳細に示しました。近似アルゴリズムと強化学習に関連する事項については基本的な内容にとどめて記述しました。強化学習等を主題としてその中でマルコフ決定過程について触れている本はいくつか見られます。しかし,マルコフ決定過程の基礎理論を中心に日本語で書かれた本としては近年では他に類するものがないと考えています。
【各章について】
1章ではマルコフ決定過程の概要を,2章では基礎理論としてマルコフ連鎖を中心として確率過程について述べています。3章から5章では,有限期間期待利得問題,無限期間総割引期待利得問題,平均利得問題のそれぞれについて,最適政策導出に関する理論と,最適政策を求めるアルゴリズムについて詳細に述べています。6章では連続時間上のセミマルコフ決定過程について述べ,7章では部分観測可能マルコフ決定過程に関する基礎的な事項を示しています。8章では,より発展的な内容として,大規模問題における近似アルゴリズムの観点からの強化学習へのアプローチ,また最適性方程式から導かれる最適政策のもつ性質の理論的導出について触れています。 - 目次
-
1. マルコフ決定過程の概要
1.1 ORと確率モデル
1.2 動的計画法
1.3 マルコフ決定過程
1.4 定式化の例
1.5 マルコフ決定過程の拡張と発展
2. マルコフ連鎖と再生過程
2.1 離散型確率変数
2.1.1 確率,期待値,分散
2.1.2 条件付き確率
2.1.3 独立
2.1.4 離散型確率変数の例
2.2 連続型確率変数
2.2.1 分布関数
2.2.2 期待値,分散,独立,条件付き確率
2.2.3 指数分布の性質
2.3 離散時間マルコフ連鎖
2.3.1 推移確率
2.3.2 状態の分類
2.4 周期
2.5 マルコフ連鎖の定常確率と極限確率
2.6 有限マルコフ連鎖
2.7 再生過程
2.8 再生報酬過程
2.9 マルコフ報酬過程
2.10 セミマルコフ過程
2.11 連続時間マルコフ連鎖
2.11.1 極限確率と定常確率
2.11.2 一様化
3. 有限期間総期待利得マルコフ決定過程
3.1 有限期間総期待利得問題
3.2 最適性方程式
3.3 値反復法
3.4 数値例
4. 総割引期待利得マルコフ決定過程
4.1 無限期間総割引期待利得
4.2 最適性方程式と理論的性質
4.3 計算アルゴリズム
4.3.1 値反復法
4.3.2 政策反復法
4.3.3 修正政策反復法
4.3.4 線形計画法
5. 平均利得マルコフ決定過程
5.1 平均利得
5.1.1 平均利得の上極限,下極限
5.1.2 可算無限状態のとき
5.1.3 定常マルコフ政策
5.1.4 平均利得と定常マルコフ政策
5.2 平均利得に関する関係式
5.3 相対値と平均利得
5.4 総割引期待利得と平均利得の関係
5.5 マルコフ決定過程の分類
5.6 計算アルゴリズム(単一連鎖の場合)
5.6.1 値反復法
5.6.2 政策反復法
5.6.3 修正政策反復法
5.6.4 線形計画法
5.7 計算アルゴリズム(多重連鎖の場合)
5.7.1 値反復法
5.7.2 政策反復法
5.7.3 線形計画法
6. セミマルコフ決定過程
6.1 セミマルコフ決定過程とは
6.2 総割引期待利得
6.3 平均利得
6.4 連続時間マルコフ決定過程(推移間隔が指数分布に従う場合)
6.4.1 一様化:割引期待利得規範の場合
6.4.2 一様化:平均費用規範の場合
6.4.3 例
7. 部分観測可能マルコフ決定過程
7.1 部分観測可能マルコフ決定過程とは
7.2 信念
7.3 定式化
7.4 値関数の線形性
7.5 ベクトル集合の生成
8. マルコフ決定過程の展開
8.1 近似最適化アルゴリズム
8.2 強化学習とマルコフ決定過程
8.2.1 状態価値と行動価値
8.2.2 TDアルゴリズム
8.2.3 Sarsa,Q学習
8.2.4 TD(λ),Sarsa(λ)アルゴリズム
8.3 決定直後の状態を用いた近似アルゴリズム
8.4 最適政策の性質
8.4.1 客の到着許可問題
8.4.2 最適政策の持つ性質の証明
引用・参考文献
索引more - 著者からのメッセージ
- マルコフ決定過程の理論の中でも特に重要な点に絞って詳細に記述しました。古典的な内容ではありますが,お役に立つことが出来れば著者として望外の喜びです。
- キーワード
- 確率,確率過程,オペレーションズ・リサーチ,動的計画法,状態,決定,マルコフ連鎖,再生過程,マルコフ決定過程,クラス,最適化,部分観測可能,最適政策,平均利得,無限期間総割引期待利得,有限期間期待利得,セミマルコフ決定過程,近似最適化,強化学習,Q学習,SARSA
設計工学フロンティアシリーズseries5
デジタルエンジニアリングと設計
- 乾 正知・山﨑慎太郎・乙守正樹 共著
これまでの形式とは異なる情報幾何学(τ-情報幾何学)が作れるということを平易に解説。
- 読者対象
-
測度論的確率論に興味はあるが専門家になる必要はない学部生・大学院生および研究者を対象としています。
また,情報幾何学のこれまでとは異なる取扱いに興味のある大学院生・研究者も対象としています。 - 書籍の特徴
-
測度論的確率論では,Radon-Nikodymの定理をvon Neumannによる証明に沿って他書を参照すること無く理解できるように,敢えて冗長な記述を試みました。一般的な数学書とは違って,できるだけ行間を読まないで済むように書いたつもりです。
また,通常の情報幾何学で登場するスコア関数に対する一次独立性の仮定を明確に式で書いておきました(67ページ)。さらに,確率変数による積分とパラメータ(自然座標)による微分が交換できる条件を定理の形で与えておきました(75-77ページ)。通常は,これらのことは正則条件という名の下に明示されないことが多いです。
ところで,いわゆるTsallisエントロピーは,本来ならばHavrda-Charvatエントロピーと言うべきです(123ページ)。この点を指摘した本も少ないと思います。また,この非加法的エントロピーが優加法性と劣加法性のどちらでも満たすように調整できることもあまり知られていないようです。この本では,劣加法性の場合に注目して取り扱っていきますが,スケール変換に対応する座標をうまく追加することで加法性をもつエントロピーに変換できることが具体的に示されます。 - 目次
-
1. 本書の構成
2. 測度と確率
2.1 可測空間と測度空間
2.2 用語の一般的な定義
2.3 Rieszの表現定理
2.4 Radon-Nikodymの定理
2.4.1 Lebesgueの分解定理の証明
2.4.2 Radon-Nikodymの定理の証明
2.5 確率測度
2.6 Dirac測度と離散確率
3. τ-アファイン空間
3.1 τ-関数
3.2 τ-アファイン構造
3.2.1 アファイン空間
3.2.2 平行移動
3.2.3 測度空間
3.2.4 十分統計量
3.3 アファイン座標系とτ-アファイン共役
3.3.1 τ-対数尤度
3.3.2 スコア関数
3.3.3 τ-アファイン共役
4. 経路順序確率
5. 縮約と計量
5.1 縮約
5.2 計量
5.3 Koszul接続と双対接続
5.4 接空間T_{¥check{p}}R_Ωの直交分解
5.5 Cramer-Raoの不等式
6. くり込みとエントロピー
6.1 素朴なエントロピー(発散)
6.2 くり込み
6.3 エントロピー(有限)
6.4 縮約と期待値
6.5 Havrda-CharvatエントロピーとRenyiエントロピー
6.6 ダイバージェンス
7. τ-情報幾何学におけるq-正規分布
7.1 q-正規分布
7.2 q-正規分布のBayes表現
8. τ-アファイン構造の多重性
8.1 τ-変換
8.2 q-正規分布のτ-変換
9. 非加法的エントロピー
9.1 恒等式と非加法性
9.2 べき型分布と相互情報量
10. 加法的エントロピーへの変換
10.1 加法性の回復
10.2 スケール座標の役割
11. ホログラフィー原理
11.1 計量とホログラフィー原理
11.2 加法・非加法変換
12. τ-平均
引用・参考文献
索引more - 著者からのメッセージ
-
最初の1章と2章を焦らずにじっくり納得しながら読んでもらえると,他の測度論的確率論に関する本を読むときにも,かなり敷居が下がると思います。
この本の3章以降は,測度空間に特別な平行移動を導入することで,これまでの形式とは異なる情報幾何学(τ-情報幾何学)が作れるというところがポイントになります。そこでは,マトリョーシカのような確率分布の入れ子構造も登場します。さらには,Fisher計量を部分行列として含むような不定計量が得られるのも面白いところです。もし,Mostowの剛性定理がうまく拡張できてτ-情報幾何学に適用できるようになれば,ここで構成される双曲空間の剛性とFisher計量の一意性についても何か言えるようになるはずですが,どなたか興味のある方はチャレンジしてみませんか? - キーワード
- 測度論,確率論,アファイン空間,双対構造,エントロピー,レニー・エントロピー,ツァリス・エントロピー,加法性,非加法性,べき型分布,指数型分布族,非指数型分布族,一般化ピタゴラスの定理,情報幾何学,ダイバージェンス,ルジャンドル変換,ヘルダー共役,AdS/CFT対応,余次元,不定計量,q-正規分布,くり込み,階層構造
設計工学フロンティアシリーズseries6
設計における知識と管理
- 野間口 大・來村徳信 共著
確率微分方程式に支配される確率システムを基盤とした電気・機械・プロセスシステムにおけるシステム理論、動的ゲームへの応用を解説
- 読者対象
- 確率システムを基盤とした動的ゲーム問題,および関連する数値計算について,基礎から応用まで幅広く学びたい大学院生・研究者を読者の対象としています。また,システム理論を軸として,実際の現場で活躍されている開発者も含まれます。特に,確率制御を含む動的ゲーム理論を将来的に応用してみたい技術者も対象にしています。
- 書籍の特徴
-
現在に至るまで,ダイナミクスを伴わない静的ゲームに関しては,多数の良書が存在します。一方,ダイナミクスを前提とした動的ゲームに関する書籍は,洋書では,多数の良書があるにもかかわらず,著者が知る限り,和書では中々見当たらないのが実情です。そこで,本書では,確率システムを基盤とした電気・機械・プロセスシステムにおけるシステム理論および動的ゲームへの応用について述べています。本書の前半部分では,確率システムにおける基礎となる内容から,システム理論の基盤に到るまで,広範囲に記述しています。一方,後半では,動的ゲーム理論についての結果や実装方法,関連する事例等を平易に記述しています。
【各章について】
1章では,今後,必要となる数学の基礎的内容について説明を行います。さらに,関連する表記法についても説明を行います。内容に関しては,最適化手法を重点に説明を行います。また,最適解を得るために必要な数値計算法について触れ,その後,システムの安定性から始まり,システム制御理論ではおなじみの最適レギュレータ問題に関して,考察を行います。特に,最大原理や動的計画法による解法について説明を行います。また,近年のシステム制御理論の成果として重要なH_∞制御理論や線形行列不等式(LMI)について触れます。
2章では,まず,連続時間における確率過程であるウィナー過程に対して,ブラウン運動を定義し,その性質について解説します。特に,確率微分方程式や関連する伊藤の公式,無限小生成作用素について,簡易な証明を含め解説します。さらに,実際の確率システムの応用についても述べます。その後,マルコフ過程においては,マルコフジャンプ確率システムについて述べます。
3章では,初めに連続時間確率システムに対して,基本的な結果である確率システムにおける可制御性,可観測性に関して議論を行い,その後,最適レギュレータ問題として良く知られる最適制御に関する結果を与えます.また離散時間システムに対しても,同様な結果を与えます。
4章では,確率リカッチ代数方程式に見られる確率非線形行列方程式を解くための数値計算アルゴリズムについて言及します。初めに,確定システムに見られるリカッチ方程式に対して,シュール法,クラインマンアルゴリズムとして知られるニュートン法を基盤とした手法を中心に,アルゴリズムや収束に関する性質について述べます.その他,再急降下法によるアルゴリズム,座標降下法によるアルゴリズムによるもの等,代表的なアルゴリズムについて考察を行います。
5章では,物理モデルのシステムパラメータが劇的に変化する,あるいは不規則なモード遷移を伴うシステムを扱う手法として良く利用される連続時間・離散時間マルコフジャンプシステムにおける安定化や最適制御問題について考察を行います。特に,線形行列不等式理論に基づく安定性から安定化,最適制御に到るまで,最新の結果について詳細を説明します。
6章では,伊藤の確率微分方程式に基づく非線形確率システムにおける様々な制御問題を対象に,制御則を得るために必要な確率ハミルトン・ヤコビ・ベルマン方程式の導出,および数値解法を中心に考えます。また,4ステップスキームとよばれる数値計算法や,確定ハミルトン・ヤコビ・ベルマン方程式の数値解法に由来するアルゴリズムに関して,解説を行います。
最後の7章では,確率システムにおけるパレート最適戦略,ナッシュ均衡戦略,スタッケルベルグ戦略を考察します。特に,システム理論との関連,および不確定要素や環境変動に対してロバスト性を達成するための現在までの取り組みや成果について,基礎的事項も含め紹介します。その他,解析手法としての動的ゲーム理論や,不確定要素や環境変動をどのように解釈・表現すれば戦略の存在条件が定式化できるかを中心に述べます。 - 目次
-
1. 数学的準備
1.1 ベクトル・行列の性質
1.2 二次形式と微分
1.3 行列の微分
1.4 最適化
1.4.1 ラグランジュの未定乗数法
1.4.2 カルーシュ・クーン・タッカー(KKT)条件
1.4.3 ニュートン法
1.4.4 勾配法
1.5 リアプノフ安定論
1.6 最適レギュレータ
1.6.1 最大原理による導出
1.6.2 動的計画法による導出
1.7 リアプノフ代数方程式
1.8 H_∞制御
1.8.1 H_∞ノルム
1.8.2 H_∞制御問題の一般解
1.9 線形行列不等式:LMI
1.10 まとめ
2. 確率過程論
2.1 確率過程
2.1.1 ウィナー過程
2.1.2 ブラウン運動の性質
2.1.3 確率微分方程式
2.1.4 確率微分方程式によるモデル表現
2.1.5 伊藤の公式
2.1.6 例題
2.2 確率システムの安定性
2.3 シミュレーション技法
2.3.1 ブラウン運動のシミュレーション
2.3.2 オイラー・丸山近似
2.4 まとめ
3. 連続・離散時間線形確率システム
3.1 連続時間線形確率システム
3.1.1 連続時間線形確率リアプノフ代数方程式
3.1.2 連続時間線形確率システムの最適レギュレータ問題
3.2 離散時間線形確率システム
3.2.1 離散時間線形確率リアプノフ代数方程式
3.2.2 安定化
3.2.3 離散時間線形確率システムの最適レギュレータ問題
3.3 まとめ
4. 数値計算アルゴリズム
4.1 リカッチ代数方程式
4.2 確率リカッチ代数方程式
4.2.1 ニュートン法による数値計算アルゴリズム
4.2.2 LMIによる数値計算アルゴリズム
4.2.3 数値例
4.3 連立型確率リカッチ代数方程式
4.3.1 ニュートン法による数値計算アルゴリズム
4.3.2 リアプノフ代数方程式による数値計算アルゴリズム
4.3.3 座標降下法による数値計算アルゴリズム
4.4 離散型マルコフジャンプ確率システムに関する数値計算アルゴリズム
4.5 まとめ
5. マルコフジャンプ確率システム
5.1 連続時間マルコフジャンプ確率システムの安定化
5.1.1 事前結果ならびに準備
5.1.2 主要結果
5.1.3 モード非依存型制御
5.2 連続時間マルコフジャンプ確率システムの最適レギュレータ問題
5.2.1 事前結果ならびに準備
5.2.2 主要結果
5.3 離散時間マルコフジャンプ確率システムの安定化
5.3.1 事前結果ならびに準備
5.3.2 主要結果
5.4 離散時間マルコフジャンプ確率システムの最適レギュレータ問題
5.4.1 事前結果ならびに準備
5.4.2 主要結果
5.5 まとめ
6. 非線形確率システム
6.1 安定性
6.2 最適レギュレータ問題
6.2.1 有限時間の場合
6.2.2 無限時間の場合
6.3 H_∞制御
6.3.1 非線形確率有界実補題
6.3.2 非線形確率システムにおけるH_∞制御
6.4 数値解法
6.4.1 逐次近似法
6.4.2 ガラーキン・スペクトル法
6.4.3 チェビシェフ多項式の導入
6.5 まとめ
7. 動的ゲーム理論への応用
7.1 パレート最適戦略
7.1.1 確率パレート最適戦略
7.1.2 確率パレート最適戦略の解
7.2 ナッシュ均衡戦略
7.2.1 混合H_2/H_∞制御問題
7.2.2 確率ナッシュ均衡戦略
7.2.3 マルコフジャンプ確率システムにおけるナッシュ均衡戦略
7.2.4 ナッシュ均衡戦略対が存在するための必要十分条件
7.2.5 ニュートン法
7.2.6 非線形確率ナッシュ均衡戦略
7.3 スタッケルベルグ均衡戦略
7.3.1 スタッケルベルグ均衡戦略問題
7.3.2 主要結果
7.3.3 数値計算アルゴリズム
7.3.4 数値例
7.4 min-max戦略:サドルポイント均衡
7.4.1 弱拘束確率ナッシュ均衡戦略問題
7.4.2 主要結果
7.5 まとめ
引用・参考文献
索引more - 著者からのメッセージ
- 近年,原子力エネルギーから再生可能エネルギーへのシフトでは,ウィンドファームでの風車の配置問題,あるいは,それらの電力を利用したピークシフト・ピークカット問題等が知られています。さらには,複数ドローンに見られる協調制御等,動的ゲーム理論が大いに活躍できる諸問題が多く存在します。本書では,このようは現実問題を解くためのヒント,あるいは道具となる結果を網羅しています。この本によって,少しでもこの分野に興味を抱く研究者が増え,活性化することを願ってやみません。
- キーワード
- 動的ゲーム,パレート最適戦略,ナッシュ均衡戦略,スタッケルベルグ均衡戦略,フィルタ付き確率空間,標準ブラウン運動,ウィナー過程,確率微分方程式,伊藤の公式,無限小生成作用素,オイラー・丸山近似,最大原理,動的計画法,リカッチ代数方程式,線形行列不等式
設計工学フロンティアシリーズseries8
感性のモデリングと設計
- 柳澤秀吉・加藤健郎 共著
不確実な状況下での意思決定問題に生かせる多種多様な2人ゲームのモデルを解説
- 読者対象
- 不確実性下の意思決定の局面でゲーム理論を応用することに関心を持つ方の役に立つことを期待しています。線形代数,微分積分,グラフ理論,確率統計等の基礎知識を持っている方には読みやすい内容であると思います。
- 書籍の特徴
-
不確実性下の意思決定あるいは最適化問題に対する2人ゲーム理論の応用を念頭において2人非協力ゲーム理論の基礎を述べ,例を与えたものです。具体的には,2人ゼロ和有限ゲーム,2人非ゼロ和有限ゲーム,2人無限ゲーム,2人不完備情報ゲームについて解説しています。2人ゼロ和ゲームモデルにおいては最適戦略を,2人非ゼロ和ゲームモデルにおいてはナッシュ均衡戦略を,不完備情報ゲームモデルにおいてはベイズ均衡戦略を考えています。戦略の計算に慣れ親しんでもらい,モデルの特徴を掴んでもらうために数値例や問を用意しています。例の中には,最近では話題となることが少ない,古典的な2人ゲームが含まれています。また,モデル化の参考になるようにと,いくつかの意思決定問題をいくつかの2人ゲームとして定式化してモデルのバリエーションを提案しています。
【各章について】
章をまたがってタイトルが同じである例の内容は関連しています。これを踏まえた上で,例は取捨選択して読み進めることができます。また,第4 章は第6 章より後に読むことができます。 - 目次
-
本書で使用する記号について
1.意思決定とゲーム理論
1.1 不確定性の下での意思決定
1.2 戦略型のゲーム
2.2人ゼロ和有限ゲーム
2.1 行列ゲーム
2.1.1 ゲームの鞍点
2.1.2 戦略の支配
2.1.3 混合戦略
2.1.4 ミニマックス定理
2.2 行列ゲームの解法
2.2.1 図による解法
2.2.2 線形計画法による解法
2.2.3 2人定和有限ゲーム
2.3 行列ゲームの例
2.3.1 線形計画問題(その1)
2.3.2 立地ゲーム(その1)
2.3.3 関門クリア問題(その1)
2.3.4 段取りを考慮した関門クリア問題
2.3.5 タイミングゲーム(その1)
2.3.6 ポーカーゲーム(その1)
2.3.7 数合わせゲーム
2.3.8 在庫管理問題(その1)
2.3.9 ブロットー大佐ゲーム(その1)
2.3.10 数量割引問題(その1)
2.3.11 侵入者捕捉問題(その1)
2.3.12 探索と順序の問題(その1)
2.3.13 合戦と順序付けのモデル(その1)
章末問題
3.2人非ゼロ和有限ゲーム
3.1 双行列ゲーム
3.2 双行列ゲームのナッシュ均衡
3.3 双行列ゲームと意思決定
3.3.1 完全均衡点
3.3.2 ランク1のゲーム
3.4 関連した話題
3.4.1 ねじり均衡点
3.4.2 シュタッケルベルク均衡
3.4.3 双行列ゲームの相関均衡
3.4.4 進化的に安定な戦略
3.5 双行列ゲームの例
3.5.1 立地ゲーム(その2)
3.5.2 線形計画問題(その2)
3.5.3 タイミングゲーム(その2)
3.5.4 在庫管理問題(その2)
3.5.5 ブロットー大佐ゲーム(その2)
3.5.6 数量割引の問題(その2)
3.5.7 探索と順序の問題(その2)
3.5.8 合戦と順序付けのモデル(その2)
章末問題
4.無限ゲーム
4.12 人ゼロ和無限ゲーム
4.1.1 ε最適戦略
4.1.2 マクシミン戦略
4.1.3 単位正方形上のゲーム
4.1.4 凹凸ゲーム
4.2 2人無限ゲームの例
4.2.1 タイミングゲーム(その3)
4.2.2 ポーカーゲーム(その2)
4.2.3 ポーカーゲーム(その3)
4.2.4 関門クリア問題(その2)
4.2.5 資源配分ゲーム
4.2.6 円板上のゲーム
4.2.7 侵入者捕捉問題(その2)
4.2.8 探索と順序の問題(その3)
4.3 タイミングゲーム(その4)
章末問題
5.展開型のゲーム
5.1 ゲームの標準化
5.2 完全情報を持つゲーム
5.3 完全記憶を持つゲーム
5.4 混合戦略と行動戦略
章末問題
6.情報不完備ゲーム
6.1 情報不完備ゲームとベイズ均衡
6.2 ベイジアンゲームの例
6.2.1 線形計画問題(その3)
6.2.2 立地ゲーム(その3)
6.2.3 在庫管理問題(その3)
6.2.4 ブロットー大佐ゲーム(その3)
6.2.5 探索と順序の問題(その4)
6.2.6 探索と順序の問題(その5)
章末問題
7.種々の話題
7.1 純粋戦略ナッシュ均衡を持つゲーム
7.1.1 ポテンシャルゲーム
7.1.2 クールノーの複占市場
7.2 多段ゲームの例
7.2.1 確率化ゲーム
7.2.2 生存ゲーム
7.2.3 累積ゲーム
7.3 ランデブー探索
7.3.1 非対称基本モデル
7.3.2 対称ランデブー探索問題
7.3.3 直線上の3人ミニマックスランデブー探索
7.3.4 グラフ上のランデブー探索
章末問題
引用・参考文献
問および章末問題の解答
索引more - 著者からのメッセージ
- 本書で挙がった例に限らず,意思決定の局面において2人非協力ゲーム理論の応用を検討するのに本書が参考になればありがたいです。
- キーワード
- 不確実性下の意思決定,オペレーションズ・リサーチ,マクシミン戦略,2人ゼロ和ゲーム,最適戦略,線形計画法,動的計画法,2人非ゼロ和ゲーム,ナッシュ均衡,相関均衡,不完備情報ゲーム,ベイジアンゲーム,タイミングゲーム,ポーカーゲーム
設計工学フロンティアシリーズseries9
安全と安心の設計論
- 小木曽 望 著
ベイズの定理に基づく学習と,それをもとにした部分観測可能なマルコフ決定過程を詳述
- 読者対象
- 予備知識として,大学1年次での線形代数,微分・積分と初歩の確率論と数理統計学を身に着けた方
- 書籍の特徴
-
本書は,直接に知ることのできない状態に関する情報を解析するための基本的な方法として用いられるベイズの定理に基づく学習と,それをもとにした部分観測可能なマルコフ決定過程の基本的な結果と応用についてまとめた。
【各章について】
1章「確率と確率過程」:本書で必要となる確率と確率過程の基本的な用語と性質について簡単に解説する。
2章「確率的順序関係」:ベイズの定理にもとづく学習を解析する上で基本となる確率的順序関係について、とくに必要となる尤度比順序を中心に述べる。
3章「マルコフ決定過程」:多段決定過程を解析する手法である動的計画法と最適性の原理を説明し,マルコフ決定過程の基本的性質についてまとめる。
4章「ジョブサーチと確率的逐次割当問題」:マルコフ決定過程のひとつである期待値最大化問題であるジョブサーチと確率的逐次割当問題を中心に説明する。
5章「学習と情報」:部分観測可能なマルコフ連鎖を中心に,ベイズの定理にもとづく学習による事前分布と事後分布の関係などをまとめる。
6章「部分観測可能な2状態マルコフ決定過程」:部分観測可能な2状態マルコフ決定過程として,逐次解析や探索問題をはじめ最適停止問題などについて解説する。
7章「部分観測可能な逐次割当問題」:部分観測可能なマルコフ決定過程としてジョブサーチや確率的逐次割当問題,最適選択問題を取り上げ,その基本的な性質を解析する。 - 目次
-
1.確率と確率過程
1.1 確率と確率変数
1.1.1 確率空間
1.1.2 確率変数
1.1.3 期待値(平均)と分散
1.1.4 同時分布と周辺分布
1.1.5 独立
1.1.6 確率変数の和
1.1.7 特性関数
1.1.8 極限定理
1.2 条件付き確率と期待値
1.2.1 条件付き確率
1.2.2 条件付き期待値
1.3 確率分布
1.3.1 二項分布
1.3.2 ポアソン分布
1.3.3 一様分布
1.3.4 指数分布
1.3.5 ガンマ分布
1.3.6 正規分布
1.4 計数過程
1.4.1 確率過程
1.4.2 ポアソン過程
1.4.3 到着時間間隔
1.4.4 非斉次ポアソン過程
1.4.5 ポアソン過程の合成
1.5 マルコフ連鎖とマルコフ過程
1.5.1 マルコフ連鎖
1.5.2 チャップマン–コルモゴロフ方程式
1.5.3 離散時間マルコフ過程
1.6 連続時間の確率過程
1.6.1 連続時間マルコフ連鎖
1.6.2 チャップマン–コルモゴロフ方程式
1.6.3 コルモゴロフの方程式
1.6.4 出生死滅過程
2.確率的順序関係
2.1 確率順序
2.2 故障率関数と順序
2.2.1 故障率関数
2.2.2 故障率順序
2.3 尤度比順序
2.4 尤度比順序とTP_2
2.4.1 TP_2
2.4.2 MTP_2
2.4.3 シフト尤度比順序
2.5 関数類による順序関係
3.マルコフ決定過程
3.1 動的計画法
3.1.1 多段決定過程
3.1.2 最適方程式
3.1.3 最適性の原理
3.2 多段決定過程
3.2.1 確率的多段決定過程
3.2.2 定常政策とマルコフ決定過程
3.3 割引のあるマルコフ決定過程
3.3.1 最適方程式
3.3.2 最適政策
3.3.3 逐次近似法
3.3.4 政策反復法
3.4 最適支出問題
3.4.1 アウトカムと確率過程
3.4.2 確定的最適支出問題
3.5 マルコフ過程の最適支出問題
4.ジョブサーチと確率的逐次割当問題
4.1 ジョブサーチ
4.1.1 関数T_F(z)とS_F(z)
4.1.2 最適方程式と最適政策
4.1.3 リコールのあるジョブサーチ
4.2 確率的逐次割当問題
4.2.1 ハーディの補題
4.2.2 確率的逐次割当問題
4.2.3 マルコフ連鎖の確率的逐次割当問題
4.2.4 割引のある確率的逐次割当問題
4.3 ポアソン過程の確率的逐次割当問題
4.4 最適選択問題
5.学習と情報
5.1 ベイズの定理
5.1.1 ベイズの定理
5.1.2 事前分布と事後分布
5.2 共役分布族
5.2.1 ポアソン分布
5.2.2 指数分布
5.2.3 期待値が未知の正規分布
5.3 部分観測可能な2状態マルコフ連鎖
5.3.1 2状態マルコフ連鎖
5.3.2 学習プロセス
5.4 部分観測可能なマルコフ連鎖
5.4.1 可算状態のマルコフ連鎖
5.4.2 事前情報と事後情報
5.5 部分観測可能なマルコフ過程
5.5.1 離散時間マルコフ過程
5.5.2 事前情報と事後情報
5.5.3 正規分布に基づくモデル
5.6 一度に複数の値を観測する学習プロセス
5.6.1 独立な確率変数の場合
5.6.2 MTP_2の場合
6.部分観測可能な2状態マルコフ決定過程
6.1 逐次解析
6.2 探索問題
6.2.1 目的物が動かない場合
6.2.2 マルコフ連鎖の探索問題
6.3 部分観測可能な2状態マルコフ決定過程
6.3.1 部分観測可能な2状態マルコフ連鎖
6.3.2 部分観測可能な最適停止問題
6.3.3 部分観測可能な取替問題
7.部分観測可能な逐次割当問題
7.1 部分観測可能なジョブサーチ
7.2 部分観測可能な確率的逐次割当問題
7.3 部分観測可能な最適選択問題
おわりに
引用・参考文献
索引more - 著者からのメッセージ
- マルコフ決定過程や部分観測可能なマルコフ決定過程については,すでに多くの著書や論文があるが,本書はベイズの定理に基づく学習と部分観測可能なマルコフ決定過程を中心に述べたものである。必要に応じて予備知識を復習し,本書を読み進めていただければと思う。
- キーワード
- マルコフ連鎖 マルコフ過程 マルコフ決定過程 動的計画法 ベイズの定理 尤度比順序 部分観測可能 ジョブサーチ 割当問題 最適停止問題
設計工学フロンティアシリーズseries10
持続可能システムの設計論 -世界観とその展開-
- 小林英樹 著
最適な採用決定のためのいわゆる秘書問題に関する確率モデルとその周辺についての解説書。
- 書籍の特徴
-
本書は秘書問題の中で重要な位置を占める最良選択問題を中心に分かりやすく解説する。厳密な理論展開というよりは直感的理解を重んじた記述になっているので、理系学部で学ぶ微分積分と応用確率論の知識があれば十分読みすすむことができる。
【各章について】
1章「秘書問題の主要モデル」:最適化基準と利用可能な情報の組合せからなる四つの問題,すなわち無情報型最良選択問題,無情報型順位最小化問題,完全情報型最良選択問題,完全情報型順位最小化問題を紹介する。
2章「無情報型最良選択問題の展開」:無情報型最良選択問題の多方面への一般化を試みる。
3章「無情報型順位最小化問題の展開」:無情報型順位最小化問題に関係する変形モデルをいくつか紹介する。
4章「Sum–the–odds定理とその展開」:Sum–the–odds定理も無情報型最良選択問題の一般化と考えられるが,1–sla(1–stage look–ahead)ルールとの関係から興味深い応用につながる。
5章「Fergusonの秘書問題」:Fergusonの秘書問題は秘書問題のルーツといえる数当てゲームのグーゴル(Googol)と深く関係している。
6章「出現数が未知の場合の最良選択問題」:無情報型最良選択問題および完全情報型最良選択問題においては,応募者総数nは既知であった。本章では未知の場合への拡張を試みる。
7章「期間問題」:期間最大化という新しい最適化基準の下で秘書問題を考える。期間問題と最良選択問題の間の興味深い対応関係も示される。
8章「PPPとFIモデル」:秘書問題では,nを大きくしたときの特性値の挙動に大きな関心が寄せられるが,これを調べることは,完全情報型問題の場合は容易でない。この困難を克服する試みとして提案されたPPP(planar Poisson process)によるアプローチを紹介する。 - 目次
-
☆発行前情報のため,一部変更となる場合がございます
1.秘書問題の主要モデル
1.1 秘書問題
1.2 無情報型モデル
1.2.1 無情報型最良選択問題
1.2.2 無情報型順位最小化問題
1.3 完全情報型モデル
1.3.1 完全情報型最良選択問題
1.3.2 完全情報型順位最小化問題
2.無情報型最良選択問題の展開
2.1 拒否とリコール
2.1.1 Petruccelliモデル
2.1.2 もう一つの拒否モデル
2.2 候補者選択問題
2.2.1 割引を考慮したNIBC
2.2.2 坂口モデル
2.2.3 1–slaルールの最適性
2.3 利得の一般化
2.3.1 ベストあるいはセカンドベストの選択
2.3.2 セカンドベストの選択
2.4 トレーニングサンプル付最良選択問題
2.4.1 トレーニングサンプル
2.4.2 漸近挙動
3.無情報型順位最小化問題の展開
3.1 メモリの制限
3.1.1 メモリサイズ
3.1.2 メモリサイズ1のNIRM
3.1.3 無限問題
3.2 NIRMの簡易ルール
3.2.1 短縮型ルール
3.2.2 漸近挙動とNHPP
4.Sum–the–odds定理とその展開
4.1 Sum–the–odds定理
4.2 Sum–the–odds定理の一般化
4.2.1 独立でないベルヌーイ試行
4.2.2 FIBCの一般化
4.3 Sum–the–multiplicative–odds定理
5.Fergusonの秘書問題
5.1 グーゴル
5.2 Fergusonの生成ルール
5.3 Gnedinの生成ルール
6.出現数が未知の場合の最良選択問題
6.1 不確実性の導入
6.2 無情報型問題
6.2.1 Presman and Soninモデル
6.2.2 Samuel–Cahnモデル
6.2.3 Brussの連続時間モデル
6.3 完全情報型問題
6.3.1 Porosinskiモデル
6.3.2 Samuel–Cahnモデル
6.4 Petruccelliの部分情報型最良選択問題
6.4.1 PET
6.4.2 PETとPORの奇妙な一致
7.期間問題
7.1 応募者数が既知の期間問題
7.1.1 無情報型期間問題
7.1.2 完全情報型期間問題
7.2 応募者数が未知の無情報型期間問題
7.3 最良選択問題と期間問題の交互対応
8.PPPとFIモデル
8.1 PPP
8.2 FIBC
8.2.1 最適ルール
8.2.2 成功確率
8.3 PETとFIBC.2
8.3.1 最適ルール
8.3.2 成功確率
8.4 PORとFIBC
8.4.1 最適ルール
8.4.2 成功確率
付録
A.1 マルチンゲール停止定理
A.2 単調ルールの下での期待利得
引用・参考文献
あとがき
索引
more - 著者からのメッセージ
- 本書を読んで秘書問題に関心を抱いた読者にはGilbert and Mosteller(1966)を薦める。この論文は、その後の発展の萌芽となったモデルを多く含み、今なおこの分野を目指す人の必読論文であり続けている。
- キーワード
- 秘書問題 最良選択問題 順位最小化問題 期間問題 動的計画法 最適停止問題 グーゴル Sum–the–odds定理 1–slaルール PPP
設計工学フロンティアシリーズseries11
設計のための発想力
- 村上 存 著
複数の主体が関わる協力ゲーム理論の基礎から応用までを自学自習できる良書
- 書籍の特徴
- 本書は,複数の主体が関わる状況に対して,主体の協力によって得られた価値を主体間で分配するための考え方の一つである協力ゲーム理論の入門的な内容である。自学自習ができるように,複数の問と章末問題、その解答も掲載した。
- 目次
-
☆発行前情報のため,一部変更となる場合がございます
1. 多人数協力ゲーム
1.1 特性関数型協力ゲーム
1.2 特性関数の性質
1.2.1 優加法的ゲームと単調ゲーム
1.2.2 凸ゲーム
1.2.3 対称ゲーム
1.2.4 定和ゲーム
1.2.5 単純ゲーム
1.2.6 本質的ゲーム
1.2.7 平衡ゲーム
1.2.8 (n,n-1)ゲーム1
1.2.9 特性関数のメビウス変換
1.3 特性関数の話題
1.3.1 部分ゲームと全平衡ゲーム
1.3.2 双対ゲーム
1.3.3 戦略的に同値なゲーム
1.3.4 協力ゲームの被覆
1.3.5 協力ゲームの多重線型拡大
1.3.6 費用配分ゲーム
1.3.7 協力ゲームと確率
1.4 協力ゲームの解
1.4.1 協力ゲームの配分
1.4.2 解の定義
1.4.3 配分間の支配関係
1.4.4 妥当配分集合
1.4.5 公理による解の導出
1.4.6 費用配分ゲームの配分
1.4.7 解の双対性*
章末問題
2. コア
2.1 コアの定義
2.2 コアの存在条件
2.3 凸ゲームとコア
2.4 最小コア
章末問題
3. シャープレイ値
3.1 シャープレイによる定義と導出
3.1.1 シャープレイ値の導出
3.1.2 プレイヤーの順列による導出
3.1.3 ダミープレイヤーとnullプレイヤー
3.2 限界貢献性による導出
3.3 ポテンシャル関数の離散勾配
3.4 投票力指数
3.5 有権者のパワーの計算
3.5.1 シャープレイ値の表現
3.5.2 有権者のパワー
3.6 凸ゲームのシャープレイ値
3.7 確率的値*
3.8 重み付きシャープレイ値*
章末問題
4. 仁
4.1 仁の定義
4.2 仁の性質
4.3 (n,n-1)ゲームの仁
4.4 仁と線形計画法
4.5 平衡集合族による仁の導出
4.6 整合性による(準)仁の導出
4.7 単純ゲームと仁
章末問題
5. カーネルと交渉集合
5.1 交渉集合
5.2 カーネル
5.3 凸ゲームのカーネルと交渉集合
5.4 妥当配分集合に対するカーネル*
章末問題
6. コアと安定集合
6.1 安定集合
6.1.1 安定集合の定義
6.1.2 3人ゲームのコアと安定集合
6.1.3 安定集合が存在しない協力ゲーム
6.2 単純ゲームのコアと安定集合
6.3 コアと安定集合の一致
章末問題
7. 協力ゲームの応用例
7.1 最適化問題と協力ゲーム
7.1.1 最小費用生成木ゲーム
7.1.2 トラベリングセールスマンゲーム
7.1.3 最大流ゲーム
7.1.4 線形生産ゲーム
7.2 割り当てゲーム
7.2.1 ●●●
7.2.2 順列ゲーム
7.3 市場ゲーム
7.3.1 市場ゲームは全平衡ゲーム
7.3.2 限界貢献がおおむね大きいゲーム*
7.4 資産分配問題
7.4.1 破産問題と解
7.4.2 破産問題と仁
7.5 施設使用料決定問題
7.5.1 空港ゲームのシャープレイ値
7.5.2 空港ゲームの仁
7.6 在庫管理問題
7.6.1 需要不確定,1期間モデル
7.6.2 経済発注量モデル
7.7 確率的特性関数型の協力ゲーム
7.7.1 達成可能集合
7.7.2 確率的特性関数型の協力ゲームの仁
章末問題
8. 双行列ゲーム
8.1 双行列ゲームの共同戦略
8.2 ナッシュの交渉解
8.2.1 ナッシュの交渉解の公理
8.2.2 ナッシュの交渉解の存在
8.2.3 ナッシュの交渉解の他の特徴付
8.3 双行列ゲームにおけるナッシュの交渉解
8.3.1 固定基準点のナッシュの交渉解
8.3.2 変動基準点のナッシュの交渉解
8.4 譲渡可能な効用の存在
章末問題
9. 種々の話題
9.1 NTUゲーム
9.1.1 NTUゲームの定義
9.1.2 NTUゲームのコア
9.1.3 KKMS定理*
9.1.4 シャープレイのNTU値
9.2 協力ゲームとその周辺
章末問題
引用・参考文献
問および章末問題の解答
索引more - 著者からのメッセージ
- 本書を読んで秘書問題に関心を抱いた読者にはGilbert and Mosteller(1966)を薦める。この論文は、その後の発展の萌芽となったモデルを多く含み、今なおこの分野を目指す人の必読論文であり続けている。
- キーワード
- 秘書問題 最良選択問題 順位最小化問題 期間問題 動的計画法 最適停止問題 グーゴル Sum–the–odds定理 1–slaルール PPP
設計工学フロンティアシリーズseries12
設計の組織化とマネジメント
- 青山和浩・古賀 毅 編著/江口隆夫・大泉和也 共著
複数の主体が関わる協力ゲーム理論の基礎から応用までを自学自習できる良書
- 書籍の特徴
- 本書は,複数の主体が関わる状況に対して,主体の協力によって得られた価値を主体間で分配するための考え方の一つである協力ゲーム理論の入門的な内容である。自学自習ができるように,複数の問と章末問題、その解答も掲載した。
- 目次
-
☆発行前情報のため,一部変更となる場合がございます
1. 多人数協力ゲーム
1.1 特性関数型協力ゲーム
1.2 特性関数の性質
1.2.1 優加法的ゲームと単調ゲーム
1.2.2 凸ゲーム
1.2.3 対称ゲーム
1.2.4 定和ゲーム
1.2.5 単純ゲーム
1.2.6 本質的ゲーム
1.2.7 平衡ゲーム
1.2.8 (n,n-1)ゲーム1
1.2.9 特性関数のメビウス変換
1.3 特性関数の話題
1.3.1 部分ゲームと全平衡ゲーム
1.3.2 双対ゲーム
1.3.3 戦略的に同値なゲーム
1.3.4 協力ゲームの被覆
1.3.5 協力ゲームの多重線型拡大
1.3.6 費用配分ゲーム
1.3.7 協力ゲームと確率
1.4 協力ゲームの解
1.4.1 協力ゲームの配分
1.4.2 解の定義
1.4.3 配分間の支配関係
1.4.4 妥当配分集合
1.4.5 公理による解の導出
1.4.6 費用配分ゲームの配分
1.4.7 解の双対性*
章末問題
2. コア
2.1 コアの定義
2.2 コアの存在条件
2.3 凸ゲームとコア
2.4 最小コア
章末問題
3. シャープレイ値
3.1 シャープレイによる定義と導出
3.1.1 シャープレイ値の導出
3.1.2 プレイヤーの順列による導出
3.1.3 ダミープレイヤーとnullプレイヤー
3.2 限界貢献性による導出
3.3 ポテンシャル関数の離散勾配
3.4 投票力指数
3.5 有権者のパワーの計算
3.5.1 シャープレイ値の表現
3.5.2 有権者のパワー
3.6 凸ゲームのシャープレイ値
3.7 確率的値*
3.8 重み付きシャープレイ値*
章末問題
4. 仁
4.1 仁の定義
4.2 仁の性質
4.3 (n,n-1)ゲームの仁
4.4 仁と線形計画法
4.5 平衡集合族による仁の導出
4.6 整合性による(準)仁の導出
4.7 単純ゲームと仁
章末問題
5. カーネルと交渉集合
5.1 交渉集合
5.2 カーネル
5.3 凸ゲームのカーネルと交渉集合
5.4 妥当配分集合に対するカーネル*
章末問題
6. コアと安定集合
6.1 安定集合
6.1.1 安定集合の定義
6.1.2 3人ゲームのコアと安定集合
6.1.3 安定集合が存在しない協力ゲーム
6.2 単純ゲームのコアと安定集合
6.3 コアと安定集合の一致
章末問題
7. 協力ゲームの応用例
7.1 最適化問題と協力ゲーム
7.1.1 最小費用生成木ゲーム
7.1.2 トラベリングセールスマンゲーム
7.1.3 最大流ゲーム
7.1.4 線形生産ゲーム
7.2 割り当てゲーム
7.2.1 ●●●
7.2.2 順列ゲーム
7.3 市場ゲーム
7.3.1 市場ゲームは全平衡ゲーム
7.3.2 限界貢献がおおむね大きいゲーム*
7.4 資産分配問題
7.4.1 破産問題と解
7.4.2 破産問題と仁
7.5 施設使用料決定問題
7.5.1 空港ゲームのシャープレイ値
7.5.2 空港ゲームの仁
7.6 在庫管理問題
7.6.1 需要不確定,1期間モデル
7.6.2 経済発注量モデル
7.7 確率的特性関数型の協力ゲーム
7.7.1 達成可能集合
7.7.2 確率的特性関数型の協力ゲームの仁
章末問題
8. 双行列ゲーム
8.1 双行列ゲームの共同戦略
8.2 ナッシュの交渉解
8.2.1 ナッシュの交渉解の公理
8.2.2 ナッシュの交渉解の存在
8.2.3 ナッシュの交渉解の他の特徴付
8.3 双行列ゲームにおけるナッシュの交渉解
8.3.1 固定基準点のナッシュの交渉解
8.3.2 変動基準点のナッシュの交渉解
8.4 譲渡可能な効用の存在
章末問題
9. 種々の話題
9.1 NTUゲーム
9.1.1 NTUゲームの定義
9.1.2 NTUゲームのコア
9.1.3 KKMS定理*
9.1.4 シャープレイのNTU値
9.2 協力ゲームとその周辺
章末問題
引用・参考文献
問および章末問題の解答
索引more - 著者からのメッセージ
- 本書を読んで秘書問題に関心を抱いた読者にはGilbert and Mosteller(1966)を薦める。この論文は、その後の発展の萌芽となったモデルを多く含み、今なおこの分野を目指す人の必読論文であり続けている。
- キーワード
- 秘書問題 最良選択問題 順位最小化問題 期間問題 動的計画法 最適停止問題 グーゴル Sum–the–odds定理 1–slaルール PPP
設計工学フロンティアシリーズseries13
設計原論
- 藤田喜久雄 著
複数の主体が関わる協力ゲーム理論の基礎から応用までを自学自習できる良書
- 書籍の特徴
- 本書は,複数の主体が関わる状況に対して,主体の協力によって得られた価値を主体間で分配するための考え方の一つである協力ゲーム理論の入門的な内容である。自学自習ができるように,複数の問と章末問題、その解答も掲載した。
- 目次
-
☆発行前情報のため,一部変更となる場合がございます
1. 多人数協力ゲーム
1.1 特性関数型協力ゲーム
1.2 特性関数の性質
1.2.1 優加法的ゲームと単調ゲーム
1.2.2 凸ゲーム
1.2.3 対称ゲーム
1.2.4 定和ゲーム
1.2.5 単純ゲーム
1.2.6 本質的ゲーム
1.2.7 平衡ゲーム
1.2.8 (n,n-1)ゲーム1
1.2.9 特性関数のメビウス変換
1.3 特性関数の話題
1.3.1 部分ゲームと全平衡ゲーム
1.3.2 双対ゲーム
1.3.3 戦略的に同値なゲーム
1.3.4 協力ゲームの被覆
1.3.5 協力ゲームの多重線型拡大
1.3.6 費用配分ゲーム
1.3.7 協力ゲームと確率
1.4 協力ゲームの解
1.4.1 協力ゲームの配分
1.4.2 解の定義
1.4.3 配分間の支配関係
1.4.4 妥当配分集合
1.4.5 公理による解の導出
1.4.6 費用配分ゲームの配分
1.4.7 解の双対性*
章末問題
2. コア
2.1 コアの定義
2.2 コアの存在条件
2.3 凸ゲームとコア
2.4 最小コア
章末問題
3. シャープレイ値
3.1 シャープレイによる定義と導出
3.1.1 シャープレイ値の導出
3.1.2 プレイヤーの順列による導出
3.1.3 ダミープレイヤーとnullプレイヤー
3.2 限界貢献性による導出
3.3 ポテンシャル関数の離散勾配
3.4 投票力指数
3.5 有権者のパワーの計算
3.5.1 シャープレイ値の表現
3.5.2 有権者のパワー
3.6 凸ゲームのシャープレイ値
3.7 確率的値*
3.8 重み付きシャープレイ値*
章末問題
4. 仁
4.1 仁の定義
4.2 仁の性質
4.3 (n,n-1)ゲームの仁
4.4 仁と線形計画法
4.5 平衡集合族による仁の導出
4.6 整合性による(準)仁の導出
4.7 単純ゲームと仁
章末問題
5. カーネルと交渉集合
5.1 交渉集合
5.2 カーネル
5.3 凸ゲームのカーネルと交渉集合
5.4 妥当配分集合に対するカーネル*
章末問題
6. コアと安定集合
6.1 安定集合
6.1.1 安定集合の定義
6.1.2 3人ゲームのコアと安定集合
6.1.3 安定集合が存在しない協力ゲーム
6.2 単純ゲームのコアと安定集合
6.3 コアと安定集合の一致
章末問題
7. 協力ゲームの応用例
7.1 最適化問題と協力ゲーム
7.1.1 最小費用生成木ゲーム
7.1.2 トラベリングセールスマンゲーム
7.1.3 最大流ゲーム
7.1.4 線形生産ゲーム
7.2 割り当てゲーム
7.2.1 ●●●
7.2.2 順列ゲーム
7.3 市場ゲーム
7.3.1 市場ゲームは全平衡ゲーム
7.3.2 限界貢献がおおむね大きいゲーム*
7.4 資産分配問題
7.4.1 破産問題と解
7.4.2 破産問題と仁
7.5 施設使用料決定問題
7.5.1 空港ゲームのシャープレイ値
7.5.2 空港ゲームの仁
7.6 在庫管理問題
7.6.1 需要不確定,1期間モデル
7.6.2 経済発注量モデル
7.7 確率的特性関数型の協力ゲーム
7.7.1 達成可能集合
7.7.2 確率的特性関数型の協力ゲームの仁
章末問題
8. 双行列ゲーム
8.1 双行列ゲームの共同戦略
8.2 ナッシュの交渉解
8.2.1 ナッシュの交渉解の公理
8.2.2 ナッシュの交渉解の存在
8.2.3 ナッシュの交渉解の他の特徴付
8.3 双行列ゲームにおけるナッシュの交渉解
8.3.1 固定基準点のナッシュの交渉解
8.3.2 変動基準点のナッシュの交渉解
8.4 譲渡可能な効用の存在
章末問題
9. 種々の話題
9.1 NTUゲーム
9.1.1 NTUゲームの定義
9.1.2 NTUゲームのコア
9.1.3 KKMS定理*
9.1.4 シャープレイのNTU値
9.2 協力ゲームとその周辺
章末問題
引用・参考文献
問および章末問題の解答
索引more - 著者からのメッセージ
- 本書を読んで秘書問題に関心を抱いた読者にはGilbert and Mosteller(1966)を薦める。この論文は、その後の発展の萌芽となったモデルを多く含み、今なおこの分野を目指す人の必読論文であり続けている。
- キーワード
- 秘書問題 最良選択問題 順位最小化問題 期間問題 動的計画法 最適停止問題 グーゴル Sum–the–odds定理 1–slaルール PPP