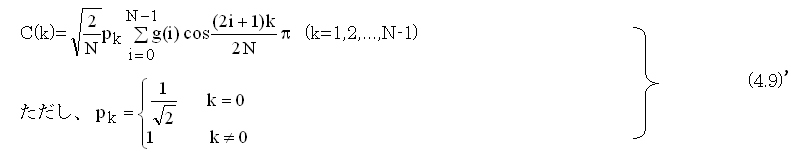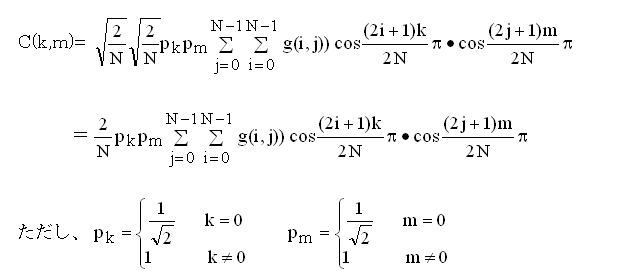アルゴリズム研究室
アルゴリズム研究室
4.2.7 コサイン変換符号化方式
離散コサイン変換(Discrete Cosine Transform:DCT)の定義は、Raoらの古典的な書籍(下記1)には、4種のタイプが書かれている。このうちの第2型が本書でも代表的な形として使用している。また、JPEGやMPEGなどの国際標準方式もこの第2型が使用されている。また、(4.7)式は第1型の類型であり、離散フーリエ変換と同じくインデックスiが整数のk倊で変化する。一方、第2型はインデックスiは奇数化されたあと、整数k倊される。奇数にずらしたことにより、コサインの値が0になることを防いであり。つまり、コサイン( )関数の変数がπ/2の倊数にならない。これは、実際の変換の計算で0があると、この部分の情報が搊失され、入力した画素値が有効に活用されないという問題を回避していることになる。なお、文献(1)にある第1型は、入力の個数をN+1個とし、N/2個の次ところで対称に折り返した対称型にしてある。
インデックスiと倊数kが偶数か奇数かで、形式的に4つの型が定義された。第1型は、両方とも偶数、第2型と第3型は片方が奇数、第4型は両方とも奇数となっている。
離散フーリエ変換に比べ、離散コサイン変換はインデックスiと倊数kの積による変数部の増え方に約2倊の違いがある。離散フーリエ変換は2πを基本としその約N倊まで増加していく。一方、離散コサイン変換の方はπを基本とし、その約N倊まで変化する。これから、同じ数Nの変換に対し、離散コサイン変換の方が離散フーリエ変換より約1/2小さい周波数で細かく分析できることガ分かる。一方、離散フーリエ変換は複素数により、コサインとサインの互いに直交した2個の成分を有しており、周波数が約1/2粗くなった分を同相と直交の2成分で表現しており、情報量が搊失されてはいない。
離散コサイン変換の定義式は、第1項のみ乗ずる係数が異なっている。そのため、第1項と他の項を分けて定義している。コサインを掛けるという意味では、変わりは無いが、上で見たようにindexを奇数としたため、正規直交性の条件が崩れるため、その補正として、第1項に別の重みをかけている。コサイン変換は直交変換であり、行列で書いた場合は、各行と別の行のベクトルの内積は全て0に成る。また、同じ行と行の内積は1になる。上記正規直交の係数補正をしないと、第1行同士の内積のみ1.0にならなくなる。
コサイン変換の定義式が多様化して使用されているのは、正規直交である所だけの差異であるため、実際の計算では、厳密な計算より、ルート2などの複素数の乗算をやめて、その後にある量子化などの演算で一括して補正をすれば、乗算が減るメリットがある。
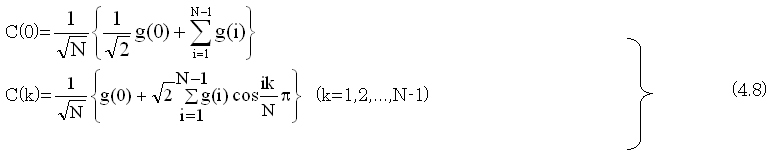
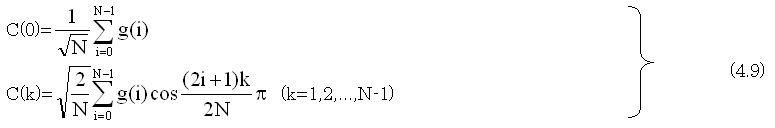
(4.8)の逆変換(Inverse DCT:IDCT)は、
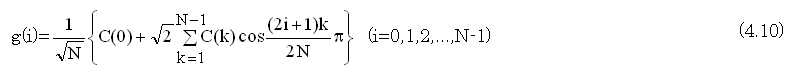
となる。
(4.9)式の係数 は正規直交化するためのもので、実際の演算では、(4.10,4.11)式のように、逆変換にて全ての係数の調整を行い、計算量の節約を図ることができる。
は正規直交化するためのもので、実際の演算では、(4.10,4.11)式のように、逆変換にて全ての係数の調整を行い、計算量の節約を図ることができる。

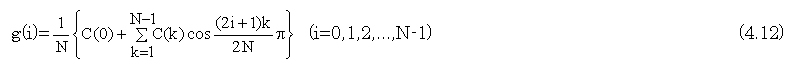
4次変換の具体的行列は、
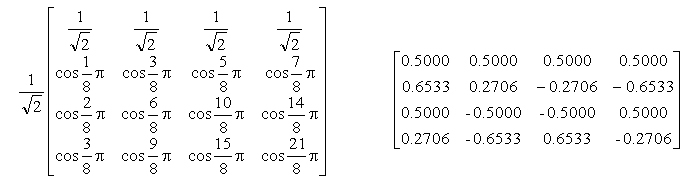
4次の逆変換は正変換の転置行列で、
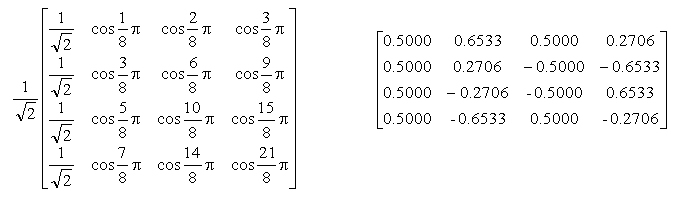
である。
8次のDCTの具体的行列は、三角関数を用いて

数値では、
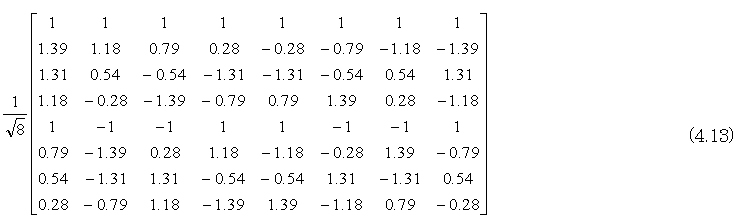
下記、参考文献(1)にある4つの型の離散コサイン変換は下記のようになっている。
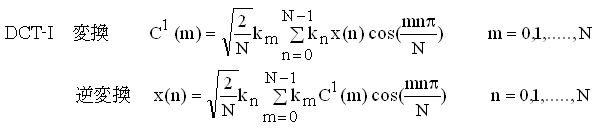

ここで、
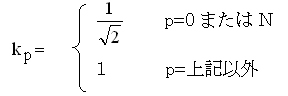
参考文献:
(1)”Discrete Cosine Transform Algorithms, Advantages,Applications”, Academic Press 1990
和訳書:「画像符号化技術-DTCとその国際基準《K.R.Rao 著 P.Yip 著、安田浩 訳、出版社:オーム社)
2次元DCT p.100 (4.16)式
2次元のDCTは、
 (4.16)
(4.16)
に示されている。
左側の[DCT]は縦変換を行い、 は[DCT]の転置行列で、横変換を担っている。具体的に、
は[DCT]の転置行列で、横変換を担っている。具体的に、
N=4の場合は、

ここで、
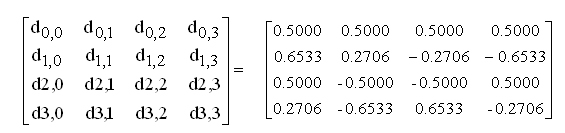
となる。
また、式で表すと、(4.9)の2つの式を、係数 を追加して一つの式に統合する。すなわち、
を追加して一つの式に統合する。すなわち、
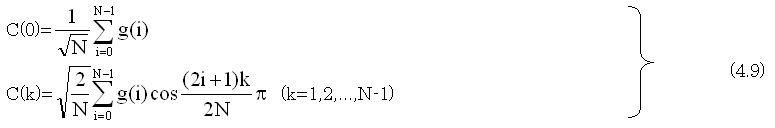
を、
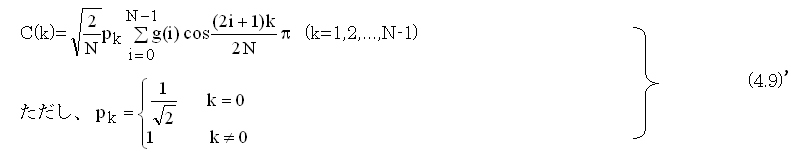
とする。2次元画像データの行列成分をg(i,j)とすると、2次元DCTは、
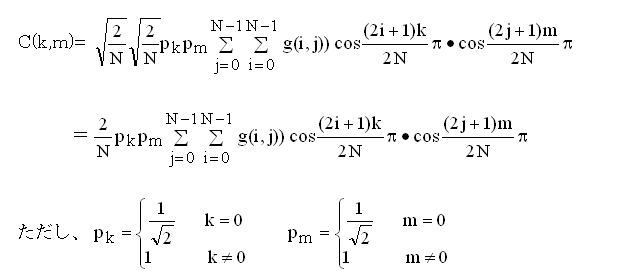
で表される。
 アルゴリズム研究室
アルゴリズム研究室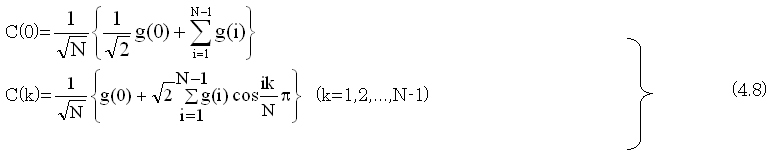
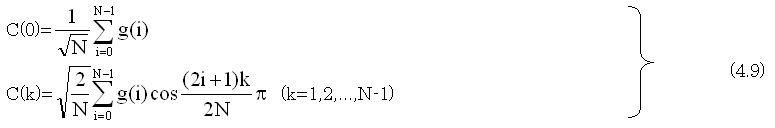
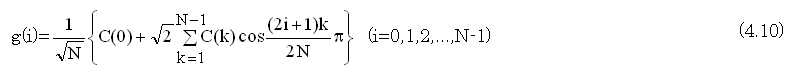
 は正規直交化するためのもので、実際の演算では、(4.10,4.11)式のように、逆変換にて全ての係数の調整を行い、計算量の節約を図ることができる。
は正規直交化するためのもので、実際の演算では、(4.10,4.11)式のように、逆変換にて全ての係数の調整を行い、計算量の節約を図ることができる。
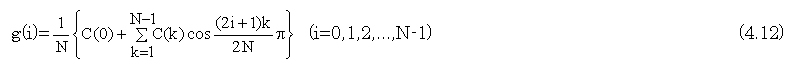
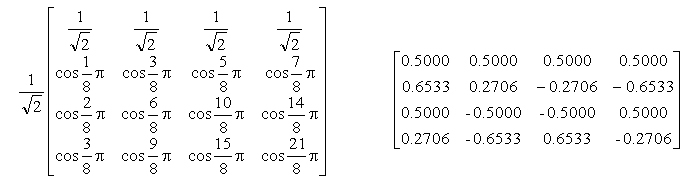
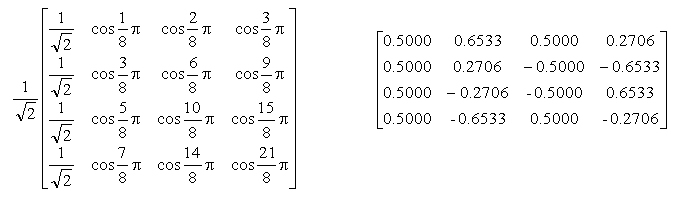


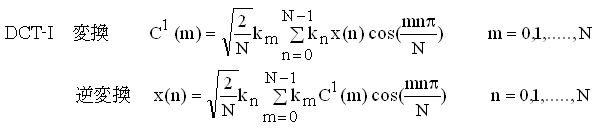

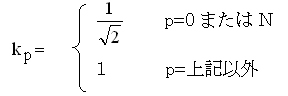
 (4.16)
(4.16)  は[DCT]の転置行列で、横変換を担っている。具体的に、
は[DCT]の転置行列で、横変換を担っている。具体的に、
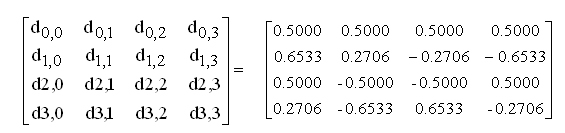
 を追加して一つの式に統合する。すなわち、
を追加して一つの式に統合する。すなわち、